Nous vous en avons déjà un peu parlé : chez Makina nous lançons une nouvelle formation en Machine Learning ainsi qu'une initiation complète au Deep Learning. En travaillant à la mise en place d'exercices, nous nous sommes lancés sur un problème connu de l'analyse d'image : la détection d'émotions.

La détection d'émotion

La détection d'émotion consiste à analyser des données (textuelles, visuelles, audio, etc.) puis à déterminer les émotions qui y sont exprimées.

La classification la plus simple de nos émotions comprend six catégories :

• la joie
• la tristesse
• la peur
• la colère
• le dégoût
• la surprise

Généralement il faut ajouter une dernière étiquette : le neutre pour le cas où aucune émotion n'est présente. Bien-sûr d'autres catégorisations existent.

Le problème sur lequel nous avons travaillé consiste à identifier une émotion à partir de photographies d'un visage issues du dataset fer2013, de petites images, avec un gros plan sur le visage et un seul visage à la fois. 

Les images que nous avons utilisées

La détection d'émotions est un domaine qui peut aller beaucoup plus loin. Par exemple, certains travaux de recherche tentent de trouver les liens qui unissent différentes personnalités politiques. En étudiant les expressions de chacun des protagonistes il est ainsi possible de repérer amitiés et inimitiés.

Les réseaux de neurones : présentation rapide

Les réseaux de neurones sont parmi les méthodes de Machine Learning les plus populaires. Leur unité de base c'est le neurone,  une fonction mathématique qui va analyser les données entrantes et produire un signal plus ou moins important selon que le neurone est sensible ou pas aux informations qu'ils traitent. 

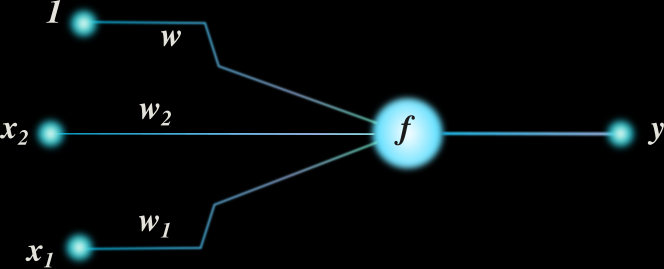
Un neurone : f(w+w1x1+w2x2) = y

Ce sont les paramètres de la fonction qui permettent cette activation. Durant l'étape d'apprentissage le réseau analyse des données pour lesquelles la solution recherchée est connue et trouve pour chaque neurone les paramètres qui lui permettront d'être pertinent.

Généralement les neurones sont organisés en couches qui transforment petit à petit les données jusqu'à en extraire toute l'information nécessaire.

Deux couches sont particulières : la couche d'entrée qui reçoit les données brutes et la couche de sortie qui produit le résultat sous la forme souhaitée. Lorsque, entre ces deux couches, le réseau de neurones possède plusieurs couches intermédiaires, nous rentrons dans le domaine du Deep Learning. Source HackerNoon

Les réseaux de neurones convolutifs

Plus connus sous leur nom anglais : Convolutional Neural Network et abrégé CNN. En analyse d'images, il s'agit de la catégorie de réseaux de neurones qui a pratiquement rendu caduques des problématiques de recherche entières, tellement leurs résultats sont impressionnants.

Leurs éléments clés sont les couches de convolutions qui permettent d'extraire les caractéristiques saillantes d'une image, en commençant par les détails et en progressant vers les structures plus globales de l'image.

Le scientifique  Michael Mozer  donne un exemple assez parlant avec un réseau entraîné pour reconnaître des chiffres tracés à la main.  L'image suivante est extraite de  l'un de ses articles : chacun des trois blocs représente 36 types de caractéristiques extraites par des couches de convolution. Celles du bloc de gauche correspondent à une vue locale de l'image, comme si vous l'observiez morceau par morceau avec une loupe. Il s'agit de caractéristiques extraites par les premières couches du réseau. Plus nous nous enfonçons dans les couches de notre réseau, plus ce dernier est capable de percevoir l'image dans sa globalité. Sur le bloc de droite nous pouvons reconnaître les chiffres.

 

D'accord, mais c'est quoi la convolution ?

Une fonction mathématique,

Bon avec cette magnifique formule issue de Wikipédia, ça fait un peu peur. Mais en fait la convolution c'est tout bête. 

Considérez que la fonction g est votre image. La fonction f elle, c'est ce nous appelons un filtre, c'est à un dire un  tableau contenant des nombres. Par exemple :

 

-1	0	1
-2	0	2
-1	0	1

L'un des deux filtres de Sobel

Réaliser cette convolution consiste à parcourir tous les blocs de **3x3** pixels de l'image, de multiplier chacun des pixels par l'un des nombres du filtre et de faire la somme des résultats de ces multiplications. La seule difficulté c'est que le pixel en haut à gauche sera multiplié par le nombre en bas à droite du tableau.

Pour chaque bloc de **3x3** pixels chaque convolution réalisée nous donne donc une nouvelle valeur. Nous obtenons une nouvelle image qui correspond à certaines caractéristiques de notre image de départ. Voici par exemple le résultat du filtre de Sobel évoqué précédement :

Image originale	Contours verticaux	Contours horizontaux

Une couche de convolution dans un réseau de neurones consiste à appliquer plusieurs filtres, sur une taille de bloc prédéfinis. Par exemple 10 filtres différents sur des blocs de **5x5** pixels.

Rien de très magique donc. La convolution n'en reste pas moins un best seller en traitement du signal, notamment parce qu'il s'agit d'une fonction mathématique disposant de propriétés très intéressantes lorsque nous souhaitons en proposer une implémentation optimisée. 

Pendant des décennies des chercheurs ont travaillé à trouver les filtres les plus pertinents. L'une des grandes forces des réseaux de neurones c'est d'être capable de trouver tout seul les filtres les plus pertinents en fonction du problème que nous leur donnons à résoudre.

Et alors, ça donne quoi ?

Nous sommes parti d'un réseau assez simple, LeNet (initialement développé pour faire de la reconnaissance de caractères) :

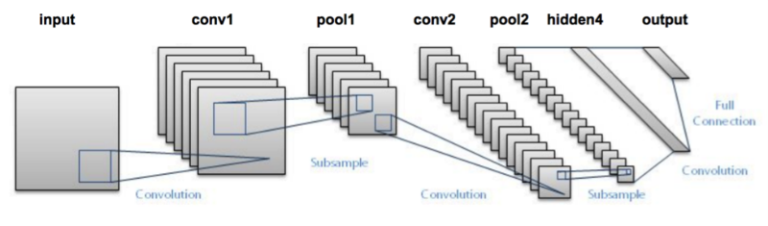
Nous l'avons légèrement modifié et après plusieurs d'entraînement notre réseau a fini par se stabiliser, avec un taux de réussite de 53%. Pas terrible comme résultat mais nous ne cherchions pas à avoir un prototype opérationnel : nous voulions un exercice qui permette à nos stagiaires de rentrer dans le Deep Learning, sa force, ses pièges et ses limites.

Les résultats, dans le détail

53% de réussite, en soi, ça ne veut pas dire grand chose. Pour comprendre ce score, il est intéressant de regarder les résultats classe par classe grâce à une matrice de confusion. Celle-ci indique pour chaque classe quel est la proportion de données correctement prédites et à quelles autres classes le reste des données ont été attribuées.

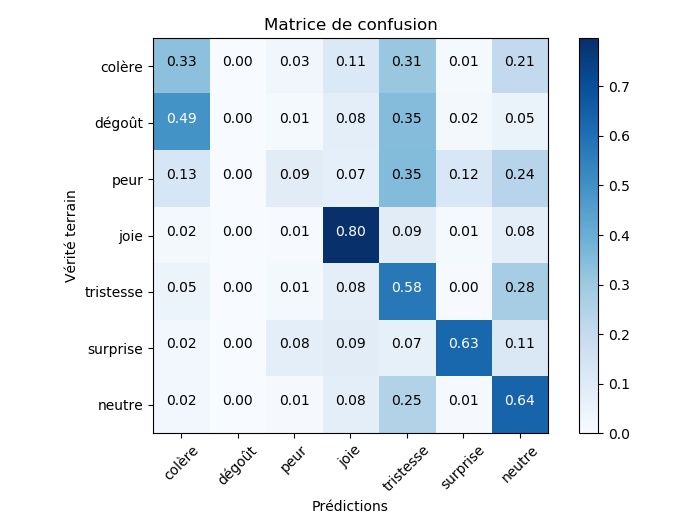
L'analyse de la matrice de confusion pour notre réseau de neurones nous amène à être beaucoup moins sévère. Le réseau reconnaît très bien les visages joyeux et ne se débrouille pas trop mal pour la surprise ou l'absence d'émotion. Là où ça se gâte, c'est sur les émotions négatives : tristesse, colère, peur et dégoût : tout cela semble bien étrange pour notre algorithme.

Des classes déséquilibrées

Une analyse plus fine de nos données d'apprentissage fournit un premier élément de compréhension. Voici le nombre de photographies dont nous disposons

• colère : 1626
• dégoût : 176
• peur : 1674
• tristesse : 1899
• joie : 2872
• surprise : 1243
• neutre : 1994

Ainsi pour la joie qui est la classe la mieux détectée, nous avons quelques 2872 images, soit au moins 900 images de plus que les autre classes. De même, avec seulement 176 photographies, il n'est pas surprenant que le réseau de neurone ne sache pas bien identifier le dégoût.

En effet l'une des particularités des réseaux de neurones est de nécessiter de très nombreuses données d'apprentissage. À titre de comparaison, la célèbre base de donnée ImageNet contient environ 3000 images pour chacune des classes.

Ce manque de données bloque notre réseau de deux manières différentes :

• en ne lui donnant pas assez d'information pour apprendre à différencier certaines classes ;
• en l'amenant à se spécialiser sur les données d'apprentissage (over-fitting) et donc à être incapable de fournir une réponse correcte pour les données de tests.

Un problème plus simple

Nous n'avons pas les données suffisantes pour réaliser l'application initiale. Par contre nous en avons assez pour essayer d'identifier les émotions positives (la joie), les émotions négatives (la tristesse, la colère, le dégoût) et les émotions neutres (la surprise et un visage sans émotion).

Sur ce problème là, les scores obtenus sont bien meilleurs : ils dépassent les 70% de réussite. Par ailleurs le réseau atteint ce score maximal bien plus rapidement : seulement une centaine d'itérations lors de l'apprentissage contre un millier dans le cas précédent.

Conclusion

Pour une application industrielle les résultats obtenus ne sont clairement pas assez bons. Mais dans le cadre de notre formation ces deux exemples fournissent une excellente introduction aux réseaux de neurones. Ils sont l'occasion d'implémenter de toutes pièces des réseaux de neurones, de charger et d'utiliser un réseau pré-entraîné, de se confronter au problème de l'overfitting et de constater 'impact négatif de classes rares (les classes pour lesquelles nous disposons de peu de données).

Enfin, le fait que les images soient de petites tailles et les données peu nombreuses, rendent réalisable une mise en pratique sur un PC de bureau et permet de conserver des temps d'exécution suffisamment courts pour laisser de la place aux expérimentations.