L’ar­chi­tec­ture d’un GPU

Même si certaines librai­ries comme Cupy, Numba ou PyOpenCL permettent de lancer des calculs pour GPU de manière « simpli­fiée », il est impor­tant de comprendre l’ar­chi­tec­ture d’un proces­seur graphique pour orga­ni­ser les calculs qu’il devra accom­plir.
À défaut les perfor­mances ne seront pas opti­males, et, même pire, le temps de calcul pour­rait être plus lent que sur CPU, comme nous venons de l’ob­ser­ver.

La mémoire

Nous l’avons déjà évoqué, mais il bon de le rappe­ler et préci­ser :

• Un proces­seur graphique calcule avec sa propre mémoire interne
• Il n’uti­lise pas la mémoire du CPU

Votre GPU doit donc dispo­ser d’une mémoire suffi­sante pour calcu­ler avec de grandes matrices/images/vecteurs, enfin, avec des données volu­mi­neuses. Sinon vous obtien­drez des Memory Over­flow et ne pour­rez mener à terme vos calculs.

Les échanges de données entre le CPU et le GPU sont lents. Il convient de les mini­mi­ser au maxi­mum, sinon ils vien­dront dimi­nuer dras­tique­ment vos perfor­mances.

Nous avons déjà vu comment obte­nir la mémoire dont dispose le GPU :

print( "%s Mega Bytes" % (gpu0.total_memory() // 1024**2))

7766 Mega Bytes

Nous pouvons reprendre la petit calcul du produit des vecteurs a et b en réali­sant réali­sant nous-mêmes le trans­fert mémoire du CPU vers le GPU afin de mieux mesu­rer ces temps.

Dans le calcul réalisé avec la fonc­tion multiply_them le temps de trans­fert des données CPU vers GPU puis GPU vers CPU était inclus dans la mesure. Ce n’était pas le cas avec cupy car les vecteurs ac, bc et destc ont été alloués direc­te­ment dans le GPU.

Le code cupy était donc plus rapide, et ceci d’un facter x16 par rapport à la fonc­tion native. C’est dire si ce temps de trans­fert des données est coûteux.

Véri­fions cela avec multiply_them en créant les vecteurs dans le GPU avant d’ap­pe­ler la fonc­tion.

La fonc­tion mem_alloc permet d’al­louer de la mémoire sur le GPU.

a_gpu = drv.mem_alloc(a.nbytes)  # Allocating a.nbytes bytes for a gpu array named a_gpu
b_gpu = drv.mem_alloc(b.nbytes)  # Same for b/b_gpu

Nous dispo­sons main­te­nant de 2 tableaux a_gpu et b_gpu alloués dans la ram du GPU.
Il convient main­te­nant de leur trans­fé­rer les données des vecteurs Numpy a et b

La fonc­tion memcpy_htod trans­fère les données du CPU vers le GPU.

• h signi­fie ici : Host, il s’agit du CPU
• d signi­fie ici : Device, il s’agit du GPU

Host et Device sont des termes de la termi­no­lo­gie CUDA pour dési­gner le CPU qui lance les calculs et le GPU qui est le péri­phé­rique (device) qui les exécute.

Nous y revien­drons tout à l’heure.

drv.memcpy_htod(a_gpu, a)  # Copying data from numpy array in RAM to GPU RAM
drv.memcpy_htod(b_gpu, b)  # Same for b

dest_gpu = drv.mem_alloc(a.nbytes)  # Also need to allocate memory for the result

Nous avons aussi alloué la mémoire pour le tableau résul­tat dest_gpu.
Par contre aucune donnée n’y a été copiée puisqu’il est utilisé pour rece­voir le résul­tat.

Relançons le calcul.

multiply_them( dest_gpu, a_gpu, b_gpu, block=(400, 1, 1), grid=(1, 1) )

Véri­fions le résul­tat en trans­fé­rant avec la fonc­tion memcpy_dtoh les données du device vers l’hôte.

dest[:] = 0
print(dest[:5])
drv.memcpy_dtoh(dest, dest_gpu)
print(dest[:5])

[0. 0. 0. 0. 0.]
[ 0.06958307 -0.01390467  1.4210043   0.84489673  0.4126398 ]

print(sum(a*b - dest))  # Ok, still good !

0.0

Mesu­rons le temps d’exé­cu­tion…

%timeit multiply_them( dest_gpu, a_gpu, b_gpu, block=(400, 1, 1), grid=(1, 1) )

6.22 μs ± 59.4 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

Nous avons gagné et dépassé les perfor­mances affi­chées par CuPy. Ce qui est normal, la classe vecteur de CuPy ajoute un peu plus de code pour gérer ses struc­tures de données alors que la fonc­tion multiply_them est la plus mini­ma­liste possible.

Cela signi­fie aussi que le temps de trans­fert des données repré­sen­tait envi­ron 95% du temps de calcul : c’est un temps très coûteux qu’il convient de mini­mi­ser au mieux.

Mais nous restons 14 fois plus lent que le CPU !

6.22/0.422

14.739336492890995

La librai­rie PyCuda dispose d’une classe gpuar­ray qui permet de mani­pu­ler des tableaux CUDA à la manière de NumPy.
Elle faci­lite aussi gran­de­ment les échanges de mémoire entre CPU et GPU.
Elle implé­mente aussi la majo­rité des opéra­teurs NumPy, comme +, -, /, * ou encore **.

Une fois les vecteurs créés, vous les utili­sez comme un tableau NumPy.

from pycuda import gpuarray

gpu_a = gpuarray.to_gpu(a)
gpu_b = gpuarray.to_gpu(b)
gpu_dest = gpu_a * gpu_b
cpu_dest = gpu_dest.get()  # transfert GPU array to CPU array of numpy type

gpu_dest[:5]  # Convert gpu_dest to numpy array too

array([ 0.06958307, -0.01390467,  1.4210043 ,  0.84489673,  0.4126398 ],
      dtype=float32)

%timeit  gpu_dest = gpu_a * gpu_b

34.6 μs ± 2.71 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

Évidem­ment cela ne change rien aux mesures obser­vées jusqu’ici…

Clai­re­ment, il nous manque encore des éléments pour comprendre comment tirer profit de ces GPU…

En fait, il y a plusieurs éléments qui entrent en jeu pour expliquer ces mesures, dont 2 majeurs ici:

• Le code utilisé sur le GPU est géné­ra­le­ment compilé par PyCuda au premier appel ce qui vient ternir les perfor­mances la première fois.
  L’uti­li­sa­tion de %prun le montrera si vous faites l’ex­pé­rience dans une nouvelle session.
  Puis les fois suivantes le code compilé est réuti­lisé depuis le cache, ce qui améliore nette­ment les mesures faites sur le GPU.
  Dans notre cas nous utili­sons %timeit qui appelle de très nombreuses fois la fonc­tion, donc le temps de compi­la­tion n’est plus visible car il est dilué sur l’en­semble des mesures.
  Il n’ex­plique donc pas ces moindres perfor­mances du GPU.
• La taille des données: ici les données sont de toutes petites taille, elles peuvent rési­der dans la mémoire cache du CPU ce qui compense large­ment le manque de cœurs sachant que la fréquence du CPU est 3 fois supé­rieure à celle du GPU et que le CPU dispose d’ins­truc­tions SIMD.

Recom­mençons l’exer­cice en faisant varier le nombre d’élé­ments des tableaux a et b et de leurs équi­va­lents gpu_a et gpu_b de 1 à 100_000_000 d’élé­ments.

Nous allons, pour chaque tableau a/b et gpu_a/gpu_b: * mesu­rer le temps de calcul de leur produit * calcu­ler les ratios temps CPU/GPU et inver­se­ment * tracer ces durées sur un graphique en fonc­tion du nombre d’élé­ments

Remarque

Pour utili­ser des tableaux d’un milliard d’élé­ments il faudrait dispo­ser de 12 Go de RAM dans le GPU car nous avons 3 tableaux de réels 32 bits (4 octets) qui doivent tenir dans la RAM de la carte graphique. Ce n’est pas le cas avec la carte utili­sée lors de la rédac­tion de ce TP.

Dans le code ci-après, nous réali­sons 10 mesures pour chaque tableau afin d’avoir un temps plus précis et conser­vons la plus petite valeur pour obte­nir les meilleurs ratios.

%matplotlib inline

import time
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
from pycuda import gpuarray
from ipywidgets import interactive



cpu_time = []
gpu_time = []
nb_items = []

for n in range(9):
    a = np.random.random(10**n).astype(np.float32)
    b = np.random.random(10**n).astype(np.float32)

    nb_items.append(n)

    # move data to gpu memory
    gpu_a = gpuarray.to_gpu(a)
    gpu_b = gpuarray.to_gpu(b)
    gpu_d = gpuarray.empty_like(gpu_a)

    cpu = []
    gpu = []

    # Do 10 timings and get min time
    for repeat in range(10):
        start = time.time()
        dest = a * b
        stop = time.time()
        duration = stop - start
        cpu.append(duration)

        start = time.time()
        gpu_d = gpu_a * gpu_b
        stop = time.time()
        duration = stop - start
        gpu.append(duration)

    cpu_time.append(min(cpu))
    gpu_time.append(min(gpu))


# Displaying

fig, ax1 = plt.subplots(figsize=(12,4))

ax1.plot(nb_items, cpu_time, label="CPU time to compute vector product", c='blue')
ax1.plot(nb_items, gpu_time, label="GPU time to compute vector product", c='red')
ax1.set_ylabel("Compute time in seconds")
ax1.legend()

ax2 = ax1.twinx()
ax2.set_ylabel("Ratio CPU vs GPU")

ax2.plot(nb_items, np.array(cpu_time) / np.array(gpu_time), label="Ratio CPU/GPU", c='orange')
ax2.plot(nb_items, np.array(gpu_time) / np.array(cpu_time), label="Ratio GPU/CPU", c='cyan')
ax2.legend(loc='center')
ax2.tick_params('y', colors='black')

fig.tight_layout()
ax1.set_xlabel('log10(vector shape)')
plt.show()

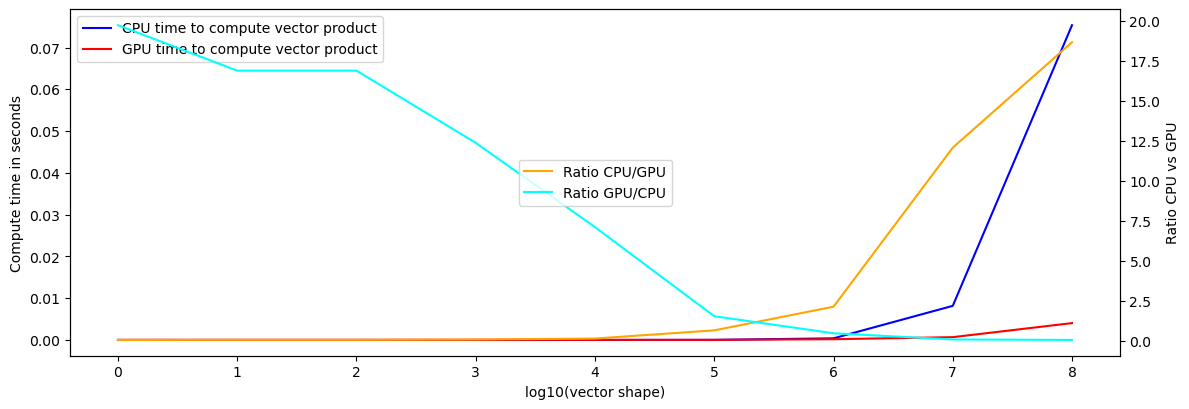
Il appa­raît clai­re­ment que sur les tableaux de moins d’un million d’élé­ments l’avan­tage est nette­ment en faveur du CPU. Mais dès que l’on dépasse ce million, le temps de calcul du CPU monte en flèche alors que pour le GPU il reste presque contant du début à la fin.

Et nous finis­sons par avoir un ratio d’un peu plus de 17.5 fois plus rapide en faveur du GPU ! C’est notre ratio théo­rique estimé précé­dem­ment !
Trop fort ! Quand la théo­rie est confir­mée par la pratique, c’est toujours un grand moment de science !

Ques­tion: Pourquoi le rapport de perfor­mance s’in­verse vers 1 million d’élé­ments en faveur du GPU ?

Cela est lié à 2 choses:

• La mémoire cache du CPU
• La grande taille du tableau qui permet d’uti­li­ser tout le poten­tiel des milliers de cœurs du GPU

---

La mémoire de votre ordi­na­teur est stockée dans des barrettes mémoire sur la carte mère. Elle ne réside pas dans le CPU comme nous l’avons vu dans le chapitre sur les concepts du paral­lé­lisme.

Cette mémoire est géné­ra­le­ment caden­cée à une fréquence infé­rieure à celle du CPU: Imagi­nons une RAM caden­cée à 1Ghz contre 3Ghz pour le CPU.
Cela signi­fie qu’en une seconde votre CPU peut effec­tuer 3 fois plus de cycles que votre RAM. Et c’est problé­ma­tique.

• Quand le CPU veut incré­men­ter le contenu d’un octet situé en RAM, il va char­ger dans un de ses registres son contenu pour le modi­fier, car la RAM ne permet que de stocker des valeurs, pas de calcu­ler direc­te­ment dessus.
  Certaines RAM disposent de telles opéra­tions, mais elles sont plus coûteuses.
• Puis le CPU incré­mente, la valeur stockée dans son registre
• Et il la redé­pose dans la RAM

La durée de ces opéra­tions sera la suivante: – 1 cycle RAM pour le trans­fert de l’oc­tet vers le CPU. Cela repré­sente 3 cycles ou le CPU ne fait rien et attend – 1 cycle de calcul pour le CPU – 1 cycle RAM pour le trans­fert du registre dans la RAM. Cela repré­sente 3 cycles ou le CPU ne fait rien et attend

Au total cette opéra­tion aura requis 7 cycles du CPU sachant que pendant 6 d’entre eux il attend la fin des opéra­tions dans la RAM.

Donc, si la RAM avait fonc­tionné à la même fréquence que le CPU l’opé­ra­tion n’au­rait duré pour le CPU que 3 cycles, contre 7. Aussi, votre CPU va tour­ner plus de 2 fois moins vite que ce qu’il pour­rait faire en raison de la lenteur de la mémoire externe. Et votre ressenti sera une fréquence de 1,5Ghz ! Ce ne sera pas un défaut du CPU mais une trop grande lenteur de votre RAM.

Pour éviter ces attentes inutiles liées au fait que la RAM dispose d’une fréquence infé­rieure, les CPU modernes possèdent une mémoire interne, dite mémoire cache de type SRAM qui est bien plus rapide et permet au CPU de tour­ner à sa fréquence opti­male. Mais elle est bien plus petite : quelques Mo au mieux car elle est stockée direc­te­ment dans le CPU et qu’il y a peu de place dans la puce – et puis elle est bien plus chère.

Donc, tant que le CPU peut faire tour­ner les données qu’il mani­pule dans sa mémoire cache, il tourne à pleine fréquence et ses perfor­mances sont opti­males.
Dès que les données à mani­pu­ler deviennent plus volu­mi­neuses, il fait de nombreux aller-retour avec la mémoire externe et ses perfor­mances se dégradent.

Si l’on compte 3 tableaux de 1 million de réels (a, b et dest) en simple préci­sion (4 octets), cela occupe très exac­te­ment 12 000 000 d’oc­tets.

Obser­vons la mémoire du CPU avec la commande lscpu ou la docu­men­ta­tion offi­cielle du proces­seur utilisé :

!lscpu| grep -i cache

Cache L1d :                             192 KiB (6 instances)
Cache L1i :                             192 KiB (6 instances)
Cache L2 :                              1,5 MiB (6 instances)
Cache L3 :                              12 MiB (1 instance)
Vulnerability L1tf:                     Mitigation; PTE Inversion; VMX conditional cache flushes, SMT vulnerable

Chaque cœur dispose de caches indi­vi­duels de 192Kox2 puis 1,5Mo et enfin peuvent parta­ger 12Mo supplé­men­taires.

Nos 3 tableaux d’un million d’élé­ments peuvent parfai­te­ment tenir dans le cache du proces­seur, au-delà il va cher­cher les données en RAM et ses perfor­mances vont se dégra­der alors que le GPU va pouvoir déployer tous ses cœurs sur ses millions de données et tirer pleine partie de son archi­tec­ture ultra paral­lé­li­sée !

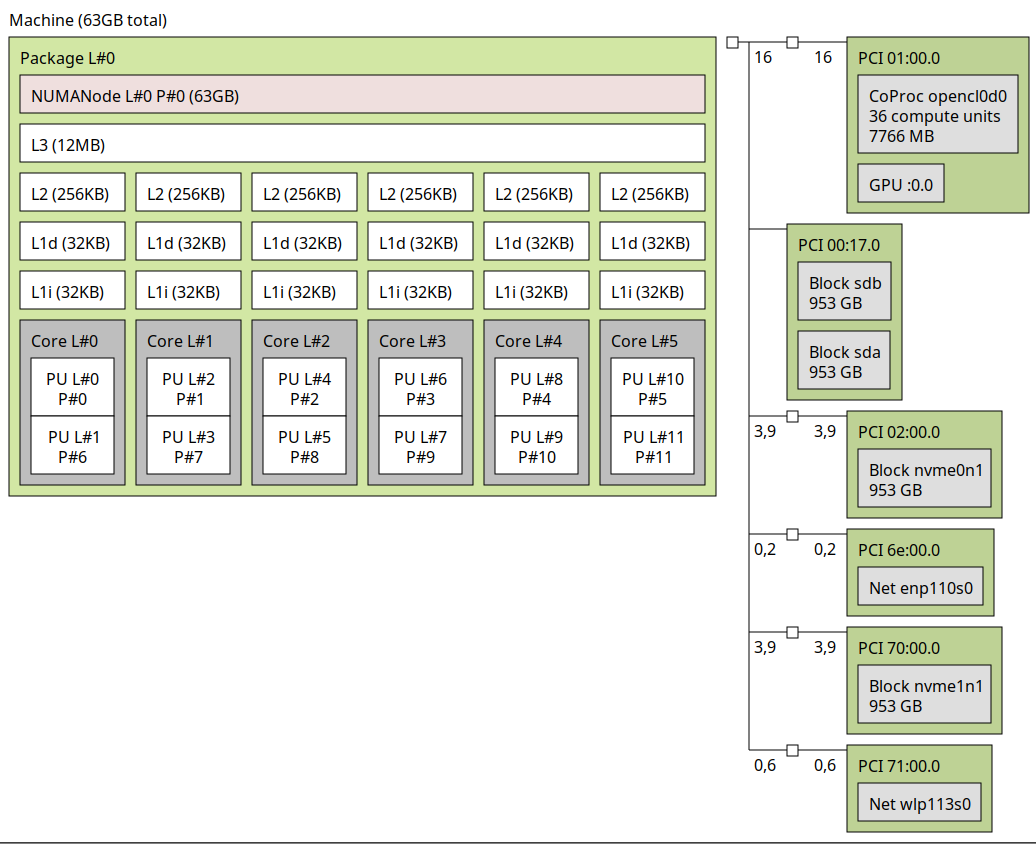
La commande hwloc-ls vous permet d’avoir une vision plus fine de la compo­si­tion de votre proces­seur.

$ hwloc-ls --of console
Machine (31GB)
  Package L#0 + L3 L#0 (12MB)
    L2 L#0 (256KB) + L1d L#0 (32KB) + L1i L#0 (32KB) + Core L#0
      PU L#0 (P#0)
      PU L#1 (P#6)
    L2 L#1 (256KB) + L1d L#1 (32KB) + L1i L#1 (32KB) + Core L#1
      PU L#2 (P#1)
      PU L#3 (P#7)
    L2 L#2 (256KB) + L1d L#2 (32KB) + L1i L#2 (32KB) + Core L#2
      PU L#4 (P#2)
      PU L#5 (P#8)
    L2 L#3 (256KB) + L1d L#3 (32KB) + L1i L#3 (32KB) + Core L#3
      PU L#6 (P#3)
      PU L#7 (P#9)
    L2 L#4 (256KB) + L1d L#4 (32KB) + L1i L#4 (32KB) + Core L#4
      PU L#8 (P#4)
      PU L#9 (P#10)
    L2 L#5 (256KB) + L1d L#5 (32KB) + L1i L#5 (32KB) + Core L#5
      PU L#10 (P#5)
      PU L#11 (P#11)

Elle propose même un aperçu graphique.

Fonc­tions Element­wi­se­Ker­nel

Nous avons utilisé la classe gpu_array qui faci­lite l’usage des tableaux pour le GPU, mais en utili­sant les fonc­tions dites Element­wi­se­Ker­nel four­nies par CUDA nous pouvons encore amélio­rer les choses.

Ces fonc­tions sont des fonc­tions C, très courtes, très rapides conçues pour ne travailler que sur un seul élément, indé­pen­dam­ment des autres, ce qui permet des opti­mi­sa­tions très avan­cées du compi­la­teur.

from pycuda.elementwise import ElementwiseKernel

gpu_mul_ker = ElementwiseKernel(
    "float *in1, float *in2, float *out",
    "out[i] = in1[i]*in2[i];",
    "gpu_mul_ker"
)

gpu_mul_ker est une fonc­tion C :

• Elle prend 3 tableaux de réels simple préci­sion en para­mètres
• Les 2 premiers sont les tableaux à multi­plier
• Le dernier contien­dra le résul­tat
• Le code tient sur une ligne, le para­mètre i est géré par CUDA, il s’agit du cœur qui fera le calcul

La fonc­tion retour­née peut être utili­sée avec des tableaux situés dans la RAM du GPU :

a = np.random.random(10**6).astype(np.float32)
b = np.random.random(10**6).astype(np.float32)

# move data to gpu memory
gpu_a = gpuarray.to_gpu(a)
gpu_b = gpuarray.to_gpu(b)
gpu_d = gpuarray.empty_like(gpu_a)

# vérifions le résultat
gpu_mul_ker(gpu_a, gpu_b, gpu_d)
gpu_d - gpu_a*gpu_b

array([0., 0., 0., ..., 0., 0., 0.], dtype=float32)

%matplotlib inline

import time
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
from pycuda import gpuarray
# from ipywidgets import interactive

cpu_time = []
gpu_time = []
nb_items = []

for n in range(9):
    a = np.random.random(10**n).astype(np.float32)
    b = np.random.random(10**n).astype(np.float32)

    nb_items.append(n)

    # move data to gpu memory
    gpu_a = gpuarray.to_gpu(a)
    gpu_b = gpuarray.to_gpu(b)
    gpu_d = gpuarray.empty_like(gpu_a)

    cpu = []
    gpu = []

    # Do 10 timings and get min time
    for repeat in range(10):
        start = time.time()
        dest = a * b
        stop = time.time()
        duration = stop - start
        cpu.append(duration)

        start = time.time()
        gpu_mul_ker(gpu_a, gpu_b, gpu_d)
        stop = time.time()
        duration = stop - start
        gpu.append(duration)

    cpu_time.append(min(cpu))
    gpu_time.append(min(gpu))


# Displaying
fig, ax1 = plt.subplots(figsize=(12,4))

ax1.plot(nb_items, cpu_time, label="CPU time to compute vector product", c='blue')
ax1.plot(nb_items, gpu_time, label="GPU time to compute vector product", c='red')
ax1.set_ylabel("Compute time in seconds")
ax1.legend()

ax2 = ax1.twinx()
ax2.set_ylabel("Ratio CPU vs GPU")

ax2.plot(nb_items, np.array(cpu_time) / np.array(gpu_time), label="Ratio CPU/GPU", c='orange')
ax2.plot(nb_items, np.array(gpu_time) / np.array(cpu_time), label="Ratio GPU/CPU", c='cyan')
ax2.legend(loc='center')
ax2.tick_params('y', colors='black')

fig.tight_layout()
ax1.set_xlabel('log10(vector shape)')
plt.show()

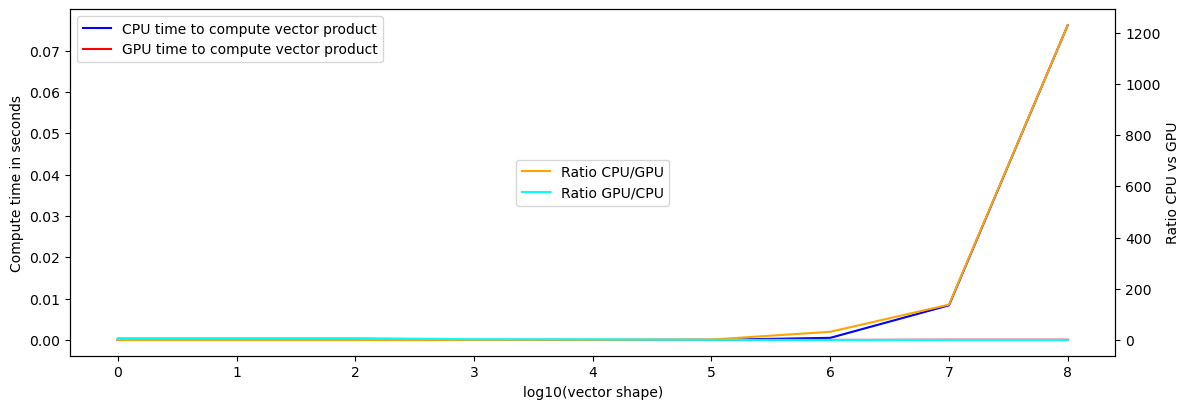
Cette fois, nous mesu­rons la toute puis­sance de la carte graphique qui est plus de 1_000 fois plus rapide que le CPU.

Sur les tableaux de moins d’un million d’élé­ments le CPU a toujours le dessus. Ce n’est plus visible en raison de l’échelle mais si vous dimi­nuez la valeur de N, vous verrez que cela n’a pas changé.

Par contre dès que nous dépas­sons le million d’élé­ments, le ratio explose en faveur du GPU, qui est envi­ron 1200 fois plus rapide que le CPU !

Utili­sez les GPU avec de très grandes volu­mé­tries de données

Pour vrai­ment béné­fi­cier de l’ar­chi­tec­ture massi­ve­ment paral­lèle de ces proces­seurs il faut pouvoir effec­tuer des calculs très nombreux en paral­lèle, sinon ils perdent tout leur inté­rêt.

C’est la conclu­sion à rete­nir !

En dessous d’un million d’élé­ments/calculs paral­lé­li­sables un GPU ne sera proba­ble­ment pas plus inté­res­sant qu’un CPU.

Noyaux (Kernels), Threads, Blocks, et Grilles (Grids)

L’ar­chi­tec­ture maté­rielle d’un GPU est diffé­rente d’un CPU.

CPU

Nous savons qu’un CPU possède des cœurs, ou unités de calcul auto­nomes, qui peuvent se décom­po­ser en threads, en géné­ral 2. Le CPU possède une mémoire cache décom­po­sée en niveau de quelques Ko ou Mo. Une partie de cette mémoire cache est propre à chaque cœur, tandis que le dernier niveau est partagé par tous les cœurs. Cette mémoire est char­gée avec les données de la RAM via des bus de données PCI. Ce qui est une source de ralen­tis­se­ment du CPU.

• Chaque cœur du CPU est auto­nome
• Dans un même cœur un seul thread est actif à la fois, et quand il est en attente de données (mémoire, disque, réseau, …), l’autre thread prend la main.

GPU

Sur les cartes NVIDIA, l’ar­chi­tec­ture logique est basée sur la notion de Kernel, Thread, Blocks et Grids.

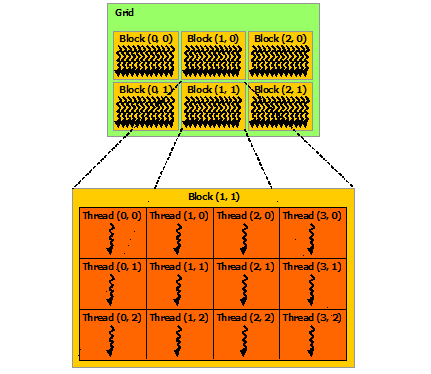
Sour­ce* Wiki­pé­dia/NVIDIA Threads, Blocs et Grilles

Nous les nomme­rons parfois avec la termi­no­lo­gie française : noyau, fil d’exé­cu­tion/fonc­tion, Bloc et Grille.

• Un Kernel ou noyau CUDA est une fonc­tion paral­lé­li­sée qui peut être lancée direc­te­ment depuis le proces­seur hôte (le CPU) sur le device (le GPU).
  Elle a pour but de lancer les calculs sur l’en­semble de la grille via des fonc­tions device.
• Une fonc­tion device est une fonc­tion appe­lée par la fonc­tion du Kernel (ou une autre fonc­tion device).
  Ces fonc­tions peuvent être compa­rées aux fonc­tions clas­siques d’un programme C, excepté qu’elles sont exécu­tées sur le GPU et initiées par une fonc­tion kernel (exécu­tée par le CPU).
• Un Thread est une fonc­tion qui s’exé­cute sur un des cœurs du GPU.
  Un thread exécute donc une fonc­tion device.
• Un Bloc/Block est un groupe de threads : dans la philo­so­phie ils sont semblables aux chunks de dask si vous connais­sez cette librai­rie
• Une Grille/Grid est un groupe de blocks : dans la philo­so­phie la grille est semblable au tableau dask composé de chunks

Votre carte graphique dispose de milliers de cœurs. 2304 pour la carte RTX2070 utili­sée dans notre exemple.

Si vous devez incré­men­ter de 1 chaque valeur d’un tableau dispo­sant d’un million d’élé­ments, vous n’avez pas assez de cœurs pour chacune des cases.

L’idée est donc de décou­per ce tableau (la grille) en blocs : * Chaque bloc possède un nombre de cœurs et travaillera sur une portion du tableau * Et les cœurs passe­ront de bloc en bloc pour trai­ter l’en­semble de la grille

Par exemple, si vous dispo­sez d’une carte avec 1000 cœurs, vous pour­riez faire des blocs de 100 cœurs chacun. Avec 10 blocs vous utili­se­riez tous vos cœurs.

Votre tableau serait alors composé de 10_000 blocs et comme vous avez 1000 cœurs, vous pour­riez lancer vos calculs en paral­lèle par paquets de 10 blocs à la fois et répé­ter ainsi 1000 fois l’opé­ra­tion.

C’est ainsi que fonc­tionnent les cartes graphiques.

Mais que de ques­tions…

• Comment choi­sir le décou­page de ma grille en blocs et de mes blocs en Threads ?
• Il y a-t-il des limites pour le nombre de blocs dans une grille, de Threads/cœurs dans un bloc ?
• Combien de blocs peut-on lancer simul­ta­né­ment en paral­lèle ?

Ce sont de bonnes ques­tions car ces éléments dépendent des spéci­fi­ca­tions de votre carte graphique.
Vous trou­ve­rez les chiffres rela­tifs à votre carte dans le tableau compute capa­blity de la docu­men­ta­tion CUDA.

Mais les ques­tions les plus redou­tables sont peut-être celles-là : * Comment utili­ser au mieux mes X cœurs si le nombre d’élé­ments de mon tableau n’est pas multiple de X, disons qu’il vaut X+1 ,.5X ou 2X-1 ? * Comment décou­per ma grille dans ce cas ?

---

La réponse suit dans l’exemple ci-après.

Strea­ming Multi­pro­ces­sors (SM)

Un Strea­ming Multi­pro­ces­sor repré­sente un ensemble de cœurs qui pour­ront trai­ter un même flux de données. C’est un peu le nombre de blocs que vous pour­riez lancer simul­ta­né­ment.

L’at­tri­but MULTI­PRO­CES­SOR_COUNT de la carte graphique indique le nombre de SM dont elle dispose :

gpu0 = drv.Device(0) 
gpu0.get_attribute(drv.device_attribute.MULTIPROCESSOR_COUNT)  # String 'MULTIPROCESSOR_COUNT' is not allowed

36

La carte peut donc trai­ter 36 flux en paral­lèle.

Le nombre de cœurs de chaque SM est défini par les capa­ci­tés de calcul de votre carte graphique.

Ces capa­ci­tés sont défi­nies par un numéro de version qui précise les fonc­tion­na­li­tés suppor­tées par le maté­riel.

gpu0.compute_capability()

(7, 5)

print(gpu0.get_attribute(drv.device_attribute.COMPUTE_CAPABILITY_MAJOR))
print(gpu0.get_attribute(drv.device_attribute.COMPUTE_CAPABILITY_MINOR))

7
5

La version des capa­ci­tés de cette carte graphique est donc 7.5.

Pour connaître les fonc­tion­na­li­tés asso­ciées il faut se réfé­rer à la docu­men­ta­tion CUDA.

La capa­cité de calcul 7.5, qui corres­pond à l’ar­chi­tec­ture Turing, permet d’uti­li­ser 64 cœurs par SM pour des calculs sur des réels en simple préci­sion et 32 cœurs par SM pour des calculs sur des réels en double préci­sion.

Soit un total de 2304 CUDA cores pour calcu­ler sur des réels simple préci­sion.
C’est bien ce que précise la page de présen­ta­tion de la carte graphique RTX 2070

print(36*64) # We find the 2304 cuda cores displayed on NVIDIA RTX 2070 web page

2304

Threads

Un Thread est une suite d’ins­truc­tions qui sont exécu­tées sur un seul cœur. Un thread n’est pas un cœur. C’est une fonc­tion. Le GPU peut rece­voir plus de threads qu’il ne possède de cœurs, tout comme un CPU exécute plus de programmes qu’il n’a de cœurs.

Blocks

Les Threads sont exécu­tés dans des unités abstraites appe­lées blocs. À" l’in­té­rieur d’un bloc leTthread peut être indexé par une deux ou trois dimen­sions : threadIdx .x, .y et .z

Un block ne peut pas conte­nir plus de 1024 Threads.

Grids

Les blocs sont quant-à eux exécu­tés dans d’autres unités abstraites appe­lées grilles. Un bloc est indexé tout comme le Thread par 3 dimen­sions dans la grille : blockIdx .x, .y et .z

Première mise en œuvre

Illus­trons ce fonc­tion­ne­ment avec la librai­rie Numba.
Comme nous l’avons vu dans Utili­ser des instruc­tions SIMD avec Python, la librai­rie Numba permet de compi­ler des fonc­tions Python et sait tirer parti des jeux d’ins­truc­tions SIMD quand votre CPU en dispose.

Et elle sait aussi compi­ler pour GPU avec le deco­ra­teur @cuda.jit si vous dispo­sez d’une carte graphique NVIDIA.

Nous allons calcu­ler la frac­tale de mandel­brot avec un autre exemple de code que nous compi­le­rons grâce à Numba sur CPU (déjà vu dans le TP sur la compi­la­tion Just In Time) puis sur GPU.

Dans un premier temps nous allons occul­ter la ques­tion la plus déli­cate : « Et si mon nombre de cœurs n’est pas multiple de mon nombre de pixels » en fabriquant une image qui respecte ces propor­tions.

Nous allons aussi igno­rer les ques­tions concer­nant les limites du nombre de blocs dans une grille…

Nous savons que nous dispo­sons de 1024 cœurs au maxi­mum par bloc. Nous crée­rons des blocs de cette taille.

Commençons par dessi­ner la frac­tale puis compi­lons-là sur CPU.

Repre­nons l’exemple de la frac­tale de Mandel­brot dont le code a été repris de l’ar­ticle Massi­vely paral­lel program­ming with GPUs et que l’on retrouve sur de nombreux autres sites.

import numpy as np
from timeit import default_timer as timer 
import matplotlib.pyplot as plt

# color function for point at (x, y)
def mandel(x, y, max_iters):
    c = complex(x, y)
    z = 0.0j
    for i in range(max_iters):
        z = z*z + c
        if z.real*z.real + z.imag*z.imag >= 4:
            return i
    return max_iters

def create_fractal(xmin, xmax, ymin, ymax, image, iters):
    height, width = image.shape

    pixel_size_x = (xmax - xmin)/width
    pixel_size_y = (ymax - ymin)/height

    for x in range(width):
        real = xmin + x*pixel_size_x
        for y in range(height):
            imag = ymin + y*pixel_size_y
            color = mandel(real, imag, iters)
            image[y, x]  = color

gimage = np.zeros((1024, 1536), dtype=np.uint8)
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
create_fractal(xmin, xmax, ymin, ymax, gimage, iters)
dt = timer() - start

print ("Mandelbrot created on CPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  
# https://matplotlib.org/examples/color/colormaps_reference.html
# je vous laisse choisir une belle palette de couleurs, je n'arrive pas à me décider

Mandelbrot created on CPU in 5.265139 s

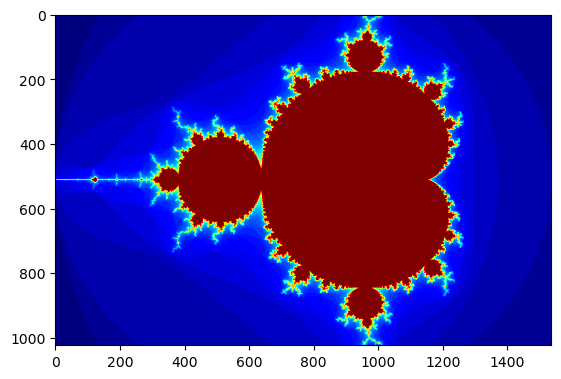
Cinq secondes pour calcu­ler une image de 1024 lignes par 1536 colonnes en pur Python inter­prété. Ce n’est pas si mal.

Nous pouvons compi­ler très faci­le­ment ce code pour CPU avec numba en ajou­tant simple­ment le déco­ra­teur @numba.jit devant chaque fonc­tion.

Celle-ci sera alors trans­for­mée pour être compi­lée lors du premier appel, puis aux appels suivants le code compilé sera utilisé.

Le premier appel est donc toujours plus lent en raison du temps de compi­la­tion. L’uti­li­sa­tion de %timeit est plus perti­nente pour des mesures de temps : cela dilue le temps de compi­la­tion entre tous les appels.

import numba

# color function for point at (x, y)
@numba.jit(nopython=True)
def mandel(x, y, max_iters):
    c = complex(x, y)
    z = 0.0j
    for i in range(max_iters):
        z = z*z + c
        if z.real*z.real + z.imag*z.imag >= 4:
            return i
    return max_iters

@numba.jit(nopython=True)
def create_fractal(xmin, xmax, ymin, ymax, image, iters):
    height, width = image.shape

    pixel_size_x = (xmax - xmin)/width
    pixel_size_y = (ymax - ymin)/height

    for x in range(width):
        real = xmin + x*pixel_size_x
        for y in range(height):
            imag = ymin + y*pixel_size_y
            color = mandel(real, imag, iters)
            image[y, x]  = color

gimage = np.zeros((1024, 1536), dtype=np.uint8)
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
create_fractal(xmin, xmax, ymin, ymax, gimage, iters)
dt = timer() - start

print ("Mandelbrot created on CPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  

Mandelbrot created on CPU in 0.333542 s

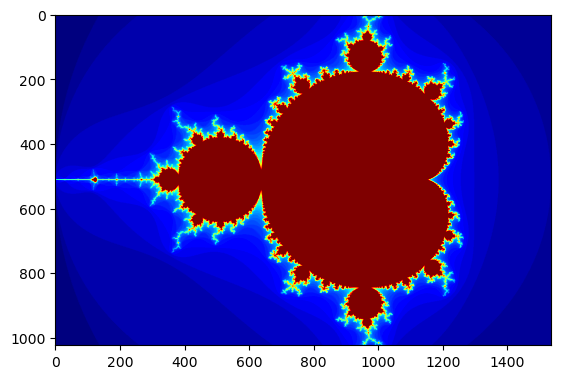
Relançons une seconde fois le code pour ne plus comp­ter le temps de compi­la­tion:

gimage = np.zeros((1024, 1536), dtype=np.uint8)
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
create_fractal(xmin, xmax, ymin, ymax, gimage, iters)
dt = timer() - start

print ("Mandelbrot created on CPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  

Mandelbrot created on CPU in 0.097677 s

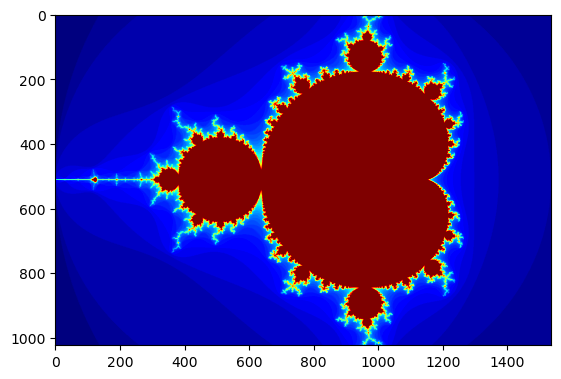
5 / 0.1  # environ 50 fois plus rapide

50.0

Sans mesu­rer le temps de compi­la­tion, le code va 50 fois plus vite.

Mais numba permet de faire encore mieux : * Les appels à la fonc­tion mandel, qui calcule la couleur d’un pixel, sont indé­pen­dants les uns des autres * Numba peut les paral­lé­li­ser avec l’op­tion parallel=True trans­mise au déco­ra­teur * Et l’uti­li­sa­tion de la fonc­tion prange pour Paral­lel-Range à la place de range qui précise que le contenu de la boucle peut être paral­lé­lisé sur diffé­rents cœurs.

Nous avons 6 cœurs physiques, nous pour­rions encore multi­plier la vitesse par 6 !

Exer­cice

Nous pouvons encore gagner plus en deman­dant à Numba de paral­lé­li­ser les appels à mandel avec l’op­tion @numba.jit(parallel=True)

Essayez de le faire.

# A vous de jouer !

Solu­tion

import numba

# color function for point at (x, y)
@numba.jit(nopython=True)
def mandel(x, y, max_iters):
    c = complex(x, y)
    z = 0.0j
    for i in range(max_iters):
        z = z*z + c
        if z.real*z.real + z.imag*z.imag >= 4:
            return i
    return max_iters

@numba.jit(parallel=True, nopython=True)
def create_fractal(xmin, xmax, ymin, ymax, image, iters):
    height, width = image.shape

    pixel_size_x = (xmax - xmin)/width
    pixel_size_y = (ymax - ymin)/height

    for x in numba.prange(width):
        real = xmin + x*pixel_size_x
        for y in numba.prange(height):
            imag = ymin + y*pixel_size_y
            color = mandel(real, imag, iters)
            image[y, x]  = color

gimage = np.zeros((1024, 1536), dtype=np.uint8)
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
create_fractal(xmin, xmax, ymin, ymax, gimage, iters)
dt = timer() - start

print ("Mandelbrot created on CPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  

Mandelbrot created on CPU in 0.375268 s

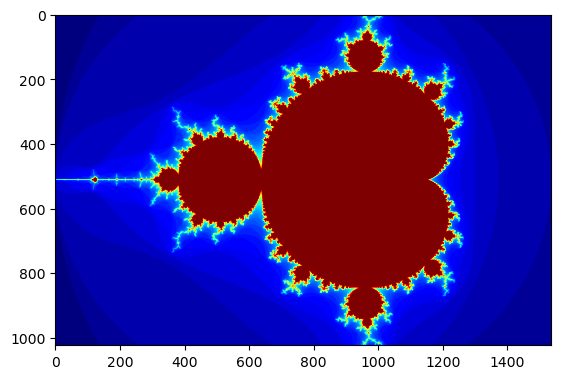
Et une seconde fois, pour ne pas comp­ter le temps de compi­la­tion :

gimage = np.zeros((1024, 1536), dtype=np.uint8)
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
create_fractal(xmin, xmax, ymin, ymax, gimage, iters)
dt = timer() - start

print ("Mandelbrot created on CPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  

Mandelbrot created on CPU in 0.017792 s

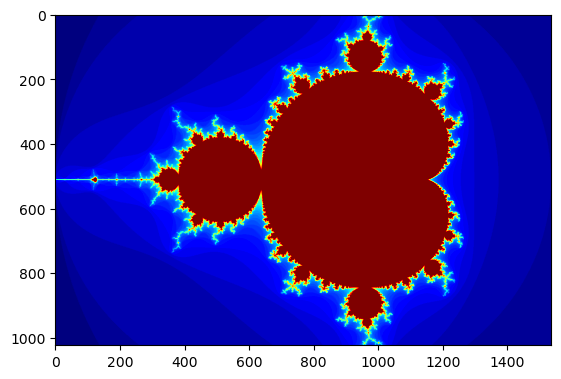
5 / 0.017

294.11764705882354

Nous frôlons le ratio théo­rique de 50 * 6 = 300 fois plus rapide que la version origi­nale en pur Python !
Vrai­ment impres­sion­nant quand la pratique du maté­riel respecte la théo­rie !

N’est-ce pas ?

Nous allons main­te­nant compi­ler ces fonc­tions avec Numba pour CUDA/NVIDIA.

Avant d’uti­li­ser numba+­cuda, nous devons libé­rer le contexte d’exé­cu­tion – notion qui sera abor­dée avec le TP PyOpenCL/PyCUDA – pris par PyCuda sur le GPU car il va gêner le fonc­tion­ne­ment de numba avec une erreur de type Non Primary Context

ctx = drv.Context.get_current()
drv.Context.detach(ctx)

Nous pouvons main­te­nant conti­nuer.

La fonc­tion mandel est appe­lée pour chaque pixel de l’image. Ce sera notre Thread qui sera exécuté sur chacun des cœurs.

Il suffit de la préfixer avec le déco­ra­teur @cuda.jit et de lui passer le para­mètre device=True qui signi­fie qu’elle sera utili­sée comme fonc­tion device, c’est-à-dire s’exé­cu­tant sur le GPU.

from numba import cuda
import numpy as np
from timeit import default_timer as timer

@cuda.jit(device=True)
def mandel(x, y, max_iters):
    c = complex(x, y)
    z = 0.0j
    for i in range(max_iters):
        z = z*z + c
        if z.real*z.real + z.imag*z.imag >= 4:
            return i
    return max_iters

Voici qui est fait pour la première. Ce n’est pas plus compliqué que pour le CPU.

La seconde fonc­tion est la fonc­tion qui lance la fonc­tion device. C’est notre fonc­tion kernel qui sera exécu­tée sur l’hôte.
La version compi­lée sera exécu­tée pour chaque Thread de la grille CUDA.

Une fois déco­rée, son invo­ca­tion est parti­cu­lière car elle va être exécu­tée pour chacun des Threads :

<fonction kernel>[grid_dim, block_dim](<params>)

• grid_dim est un tuple indiquant le nombre de blocs par grille en colonnes et lignes (et profon­deur si besoin).
  ATTEN­TION CUDA utilise les colonnes en première dimen­sion, contrai­re­ment à NumPy qui utilise les lignes.
• bloc_dim est un tuple indiquant le nombre de Threads par bloc

Il convient donc de défi­nir la struc­ture de notre grille et de nos blocs.

Nous avons choisi de travailler avec une image dont les dimen­sions sont compa­tibles avec la taille maxi­male des blocs dans ce premier exemple, pour plus de simpli­cité.

Nous savons que nous ne pouvons pas utili­ser plus de 1024 Threads par bloc. Ceci permet d’avoir des blocs carrés de 32×32, mais nous aurions pu chosir 64×16 ou tout autre couple dont le produit est 1024.

Si nous restons sur des blocs carrés (32×32), sachant que l’image fait 1536 colonnes et 1024 lignes, nous pouvons alors défi­nir une grille de 48 blocs en colonnes et 32 lignes.

1536 / 32, 1024 / 32

(48.0, 32.0)

Main­te­nant, il convient de restruc­tu­rer le code de la fonc­tion Kernel.

Celle-ci, aupa­ra­vant, utili­sait 2 boucles imbriquées pour parcou­rir toutes les colonnes puis les lignes de l’image et appe­ler la fonc­tion mandel pour chaque pixel ainsi parcouru.

Avec CUDA, elle sera appe­lée pour chaque Thread de chaque bloc de la grille. Ces boucles ne sont plus néces­saires et doivent dispa­raître.
Nous devons donc trans­for­mer le code pour calcu­ler les coor­don­nées du pixel en fonc­tion des coor­don­nées du thread dans le bloc et du bloc dans la grille.

• Les variables cuda.threadIdx.x et cuda.threadIdx.y contiennent les coor­don­nées du Thread dans le bloc.
  De 0 à 31 dans notre cas

• Les variables cuda.blockIdx.x et cuda.blockIdx.y contiennent les coor­don­nées du bloc dans la grille.
  De 0 à 47 dans notre cas pour les colonnes et de 0 à 31 pour les lignes.

• Les variables cuda.blockDim.x et cuda.blockDim.y contiennent les dimen­sions du bloc. Dans notre cas : 32 colonnes et 32 lignes

Avec ces variables, nous pouvons donc recons­ti­tuer les coor­don­nées du pixel sur lequel la fonc­tion device est exécu­tée.

# Son code peut être transformé ainsi:
@cuda.jit()
def create_fractal(xmin, xmax, ymin, ymax, image, iters):
    height, width = image.shape

    pixel_size_x = (xmax - xmin)/width
    pixel_size_y = (ymax - ymin)/height

    tx = cuda.threadIdx.x  # abscisse de 0 à 31 du Thread dans le block
    ty = cuda.threadIdx.y  # idem en ligne pour l'ordonnée
    bx = cuda.blockIdx.x   # abscisse de 0 à 47 du bloc dans la grille
    by = cuda.blockIdx.y   # ordonnée de 0 à 31 du bloc dans la grille

    # Block width, i.e. number of threads per block
    bw = cuda.blockDim.x  # largeur du bloc : nombre de Threads en colonnes dans le bloc
    bh = cuda.blockDim.y  # longueur du bloc : nombre de Threads en lignes dans le bloc

    # Recalculons les valeurs de x, y, imag et real avec les coordonnées des Threads/Blocs
    """
    # Que fait le code original ?
    for x in range(width):  # Il parcourt les colonnes de l'image avec x
        real = xmin + x*pixel_size_x  # Puis il calcule real en fonction de l'abscisse x dans l'image
        for y in range(height):  # Pour chaque colonne il parcourt les lignes
            imag = ymin + y*pixel_size_y  # Puis il calcule imag en fonction de l'ordonnée y dans l'image
            color = mandel(real, imag, iters)  # et appelle mandel pour chaque pixel avec real et imag
            image[y, x]  = color
    """
    # Maintenant, cette fonction sera exécutée sur un cœur, via un Thread, pour chaque Thread de chaque bloc de la grille
    # La position du cœur/thread dans son bloc et du bloc dans la grille indiqueront les coordonnées du pixel calculé
    # L'abscisse devient : position en X du Thread dans le bloc + position du bloc en X dans la grille * largeur du bloc en colonne

    # Par exemple, le 36ème pixel (abscisse x=35)  aura pour abscisse de thread 3 dans le bloc 1 dont la largeur est 32 : 3 + 1 * 32 = 35
    x = tx + bx * bw 
    y = ty + by * bh

    real = xmin + x*pixel_size_x
    imag = ymin + y*pixel_size_y

    image[y, x]  = mandel(real, imag, iters)

Ici le code est vrai­ment très diffé­rent, c’est une fonc­tion element­wize qui s’ap­plique élément par élément.

Pour compi­ler votre code Python avec Numba sur GPU, il faut vrai­ment passer par cette étape de restruc­tu­ra­tion/atomi­sa­tion du code par élément du tableau.
Ceci le rend moins portable, mais pas plus long.

L’ef­fort intel­lec­tuel est consé­quent, prenez le temps de dessi­ner le proces­sus dans le code si vous avez du mal à le comprendre.

Main­te­nant, exécu­tons-le pour véri­fier que cela fonc­tionne bien et mesu­rer s’il mérite la peine que nous nous sommes donnés…

import matplotlib.pyplot as plt
gimage = np.zeros((1024, 1536), dtype=np.uint8)
blockdim = (32, 32)
griddim = (48, 32)  # la grille utilise les colonnes en 1ere coordonnée
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
d_image = cuda.to_device(gimage)
create_fractal[griddim, blockdim](xmin, xmax, ymin, ymax, d_image, iters)
gimage = d_image.copy_to_host()
dt = timer() - start

print("Mandelbrot created on GPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  

Mandelbrot created on GPU in 0.219687 s

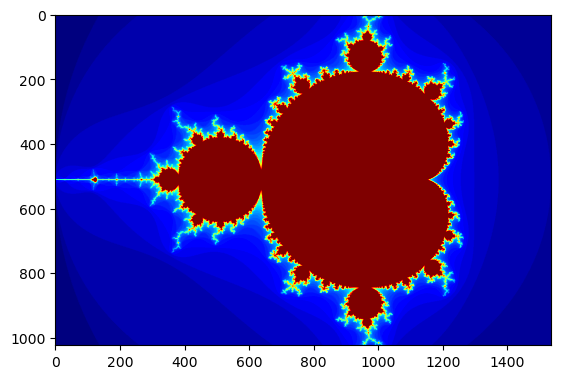
N’ou­bliez pas la seconde exécu­tion pour ne pas comp­ter le temps de compi­la­tion…

import matplotlib.pyplot as plt
gimage = np.zeros((1024, 1536), dtype=np.uint8)
blockdim = (32, 32)
griddim = (48, 32)  # la grille utilise les colonnes en 1ere coordonnée
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
d_image = cuda.to_device(gimage)
create_fractal[griddim, blockdim](xmin, xmax, ymin, ymax, d_image, iters)
gimage = d_image.copy_to_host()
dt = timer() - start

print("Mandelbrot created on GPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  

Mandelbrot created on GPU in 0.006086 s

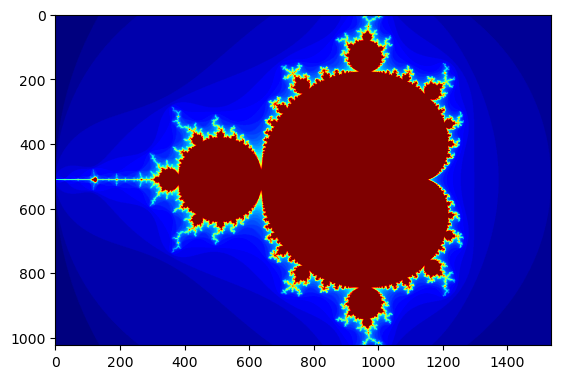
Nous sommes près de 600 fois plus rapides que le code Python d’ori­gine, et cela inclut le temps de trans­fert CPU-GPU qui est coûteux.

5 / 0.006

833.3333333333334

Si vous souhai­tez juste mesu­rer le temps de la fonc­tion create_fractal seule il faut savoir que son appel n’est pas bloquant. Pour votre CPU le GPU est un co-proces­seur, un péri­phé­rique, il lui trans­met les ordres et conti­nue sa vie sans attendre le retour.

Donc %timeit create_fractal[griddim, blockdim](xmin, xmax, ymin, ymax, d_image, iters) seul n’in­dique­rait que le temps de lance­ment de la fonc­tion, même si elle prend des heures à s’exé­cu­ter.
Il faut appe­ler la fonc­tion cuda.synchronize() pour deman­der au CPU d’at­tendre la fin des tâches du GPU.

%%timeit 
create_fractal[griddim, blockdim](xmin, xmax, ymin, ymax, d_image, iters)
numba.cuda.synchronize()

2.72 ms ± 20.3 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

5 / 0.0027  # 1800 fois plus rapide ! Merci numba.

1851.8518518518517

Si après le calcul vous trans­fé­rez des données du GPU au CPU cela bloque aussi votre CPU sur l’at­tente du résul­tat et les temps affi­chés sont alors fiables.

Nous avons main­te­nant un code plus de 1700 fois plus rapide que celui initia­le­ment réalisé en pur python. Cela en valait la peine !

Magni­fique !

Mais, main­te­nant, comment dimen­sion­ner la grille si le tableau n’est pas multiple du nombre de cœurs ?

D’au­tant plus que dans notre exemple nous utili­sons des blocs de 1024 cœurs, or nous avons 2304 cœurs, ce qui signi­fie que nous ne pouvons faire que 2 blocs et que poten­tiel­le­ment 280 cœurs ne sont pas utili­sés.

Notre décou­page n’est pas idéal.

Bien utili­­ser les Strea­­ming Multi­­pro­­ces­­sors (SM)

Le code fonc­tionne bien mais n’est pas encore parfait : Nous ne gérons pas correc­te­ment les proces­seurs de flux (Strea­ming Multi­pro­ces­sors).

Le code exécuté sur la carte GPU l’est au travers des SM qui ne peuvent utili­ser qu’un nombre maxi­mal (puis­sance de 2 – à véri­fier) de Threads. Le nombre de SM est aussi limité.

D’autre part, ici tout s’est bien passé car la taille de l’image est multiple du nombre de threads par bloc. Mais comment gérer notre problème si l’image possède une ligne et une colonne de plus ?

L’ar­ticle Writing cuda kernels de la présen­ta­tion GTC Numba l’ex­plique.

Pour comprendre l’al­go­rithme à mettre en œuvre dans ce cas, nous allons imagi­ner cette confi­gu­ra­tion très simple :

• Une carte graphique :
  • Dotée de 6 cœurs unique­ment
  • Pouvant tota­li­ser des blocs d’au plus deux Threads par sm
  • Ne pouvant dépas­ser 3 SM
• Une matrice de 11 colonnes et 2 lignes sur laquelle nous souhai­tons appliquer un calcul element­wise.

L’idée va être la suivante : * On crée a minima autant de blocs qu’il y a de SM, donc 3 ici. Que nous nommons ici B0, B1 et B2, ils repré­sentent la grille !
* On choi­sit une dispo­si­tion des threads dans un bloc qui semble cohé­rente avec la matrice, dans notre schéma ci-dessous : 2 colonnes, 1 ligne.

Avec 3 blocs de 2 Threads, cela fait 6 Threads dans la grille pour 22 éléments :

• Le Bloc B0 (en vert) possède 2 Threads numé­ro­tés t0, t1 dans celui-ci
• Le Bloc B1 (en jaune) possède 2 Threads numé­ro­tés t0, t1 dans celui-ci
• Le Bloc B2 (en bleu) possède 2 Threads numé­ro­tés t0, t1 dans celui-ci

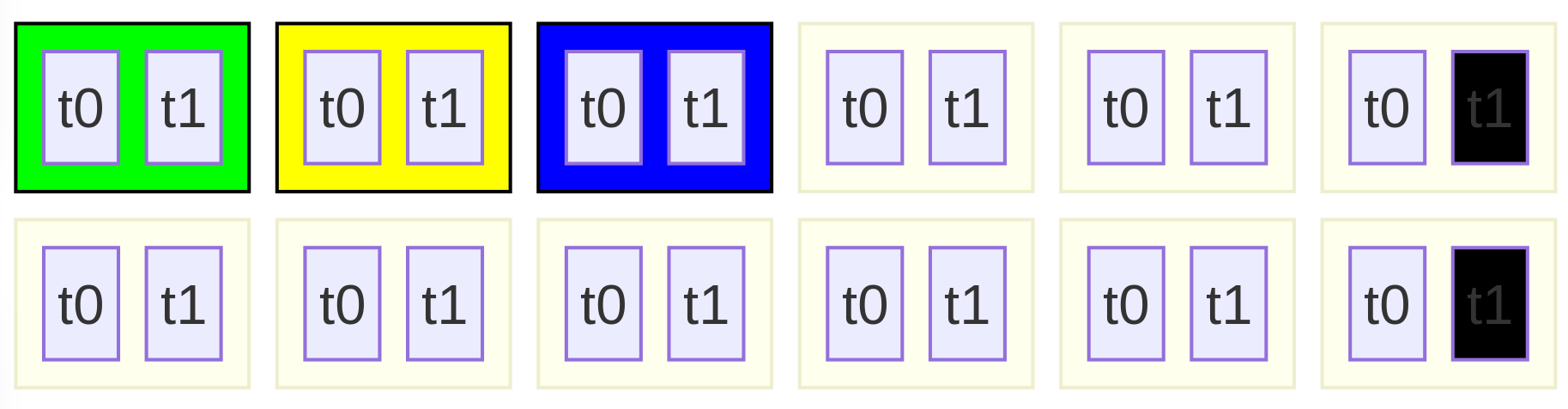
3 blocs de 2 threads

La grille est plus petite que la matrice à calcu­ler !
Beau­coup d’élé­ments passe­raient à la trappe si nous nous arrê­tions là…

Aussi chaque Thread ne s’oc­cu­pera pas dans son bloc que d’un seul élément du tableau mais de plusieurs.

Dans un bloc, chaque Thread s’oc­cu­pera : * De l’élé­ment qu’il désigne * Le Thread t0 du bloc B0 s’oc­cu­pera de l’élé­ment en 0,0
* Le Thread t1 du bloc B0 s’oc­cu­pera de l’élé­ment en 1,0 # colonne d’abord avec CUDA * Le Thread t0 du bloc B1 s’oc­cu­pera de l’élé­ment en 2,0 * Le Thread t1 du bloc B1 s’oc­cu­pera de l’élé­ment en 3,0 * Le Thread t0 du bloc B2 s’oc­cu­pera de l’élé­ment en 4,0 * Le Thread t1 du bloc B2 s’oc­cu­pera de l’élé­ment en 5,0 * Mais aussi des éléments situés à la même posi­tion déca­lés de la hauteur et largeur de la grille en éléments (6, 1) tant que les dimen­sions de la matrice ne sont pas dépas­sées * Le Thread t0 du bloc B0 s’oc­cu­pera donc aussi des éléments (0, 1), (6, 0) et (6, 1) * Le Thread t1 du bloc B0 s’oc­cu­pera donc aussi des éléments (1, 1), (7, 0) et (7, 1) * … * Le Thread t1 du bloc B2 s’oc­cu­pera donc aussi de l’élé­ment (5, 1) et ce sera tout car après il serait hors de la matrice

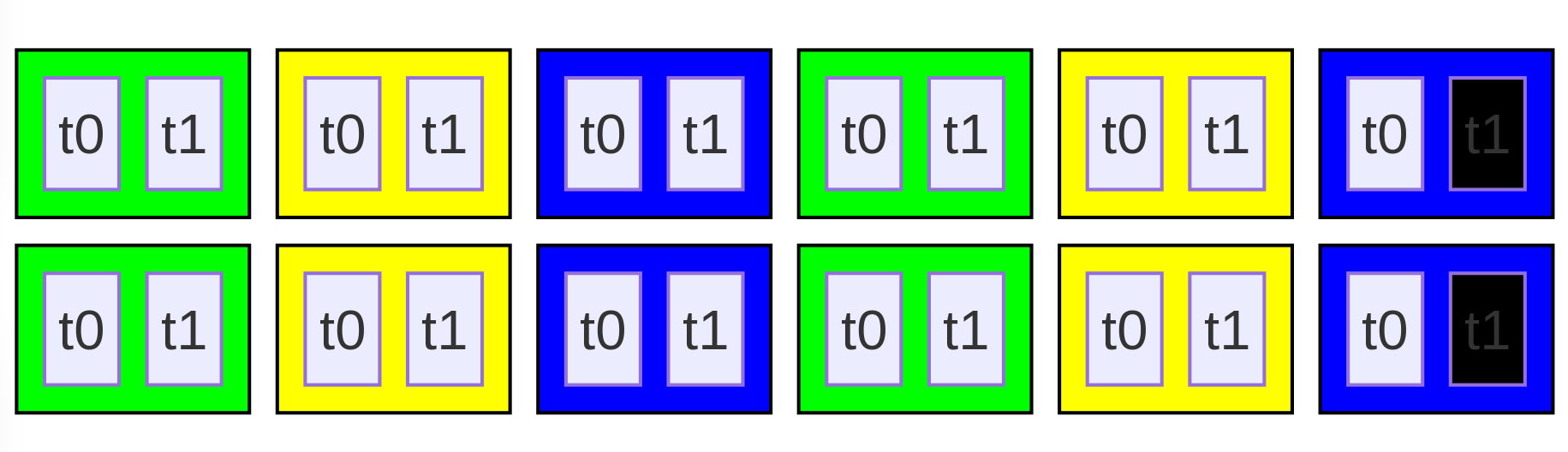
3 blocs de 2 threads :

Voici l’exemple de writing cuda kernels qui addi­tionne deux vecteurs de 100 000 éléments, nombre d’élé­ments qui n’est pas un multiple du nombre de cœurs de la carte…

from numba import cuda

@cuda.jit
def add_kernel(x, y, out):
    tx = cuda.threadIdx.x # this is the unique thread ID within a 1D block
    bx = cuda.blockIdx.x  # Similarly, this is the unique block ID within the 1D grid

    block_width = cuda.blockDim.x  # number of threads per block
    grid_width = cuda.gridDim.x    # number of blocks in the grid

    start = tx + bx * block_width
    step_x = block_width * grid_width

    # assuming x and y inputs are same length
    for i in range(start, x.shape[0], step_x):
        out[i] = x[i] + y[i]

import cupy as cp

n = 100_000
x = cp.arange(n).astype(np.float32)
y = 2 * x
out = cp.empty_like(x)

threads_per_block = 64
blocks_per_grid = 36  # Utilisation de 30 SM

add_kernel[blocks_per_grid, threads_per_block](x, y, out)
print(out[:10])
print(out[-10:])

[ 0.  3.  6.  9. 12. 15. 18. 21. 24. 27.]
[299970. 299973. 299976. 299979. 299982. 299985. 299988. 299991. 299994.
 299997.]

Ici, le nombre de blocs est égal au nombre de SM : 36.
Il y a 64 Threads par SM, soit 36*64 = 2304 cœurs de la carte graphique utili­sés

L’idée est qu’un Thread ne mettra pas à jour qu’une seule case mémoire, mais sa case mémoire et toutes les suivantes déca­lées du nombre total de cœurs utili­sés (step_x)

Comme la boucle for itère de la posi­tion courante du thread jusqu’à la fin du tableau avec un pas de step_x nous ne risquons pas de dépas­ser la fin du tableau.

Voici les recom­man­da­tions des déve­lop­peurs Numba/CUDA :

• La taille d’un bloc doit être un multiple de 32 Threads, avec des tailles de bloc typiques entre 128 et 512 Threads par Bloc.
• La taille de la grille doit permettre d’uti­li­ser l’in­té­gra­lité du GPU dans la mesure du possible
  N’hé­si­tez pas à avoir plus de blocs que de SM : 2 à 4 fois plus est un bon point de départ
• L’exé­cu­tion répé­tée de la fonc­tion Kernel pour démar­rer chaque Thread génère un surcout propor­tion­nel au nombre de Blocs/Threads.
  Il est donc préfé­rable de ne pas lancer une grille dont le nombre de Threads est égal au nombre d’élé­ments d’en­trée lorsque la taille de l’en­trée est très impor­tante.
  *Dans notre premier exemple avec la frac­tale, c’est exac­te­ment ce que nous avons fait et ce qu’il ne fallait pas faire !

Exer­cice

Repre­nez le code de la fonc­tion kernel pour l’adap­ter à ces recom­man­da­tions et permettre de calcu­ler sur une image dont les dimen­sions ne sont pas des multiples du nombre de cœurs.

# A vous de jouer !

Solu­tion

# Son code peut être transformé ainsi:
@cuda.jit()
def create_fractal(xmin, xmax, ymin, ymax, image, iters):
    height, width = image.shape

    pixel_size_x = (xmax - xmin)/width
    pixel_size_y = (ymax - ymin)/height

    tx = cuda.threadIdx.x  # abscisse de 0 à 31 du thread dans le block
    ty = cuda.threadIdx.y  # idem en ligne pour l'ordonnée
    bx = cuda.blockIdx.x   # abscisse de 0 à 47 du bloc dans la grille
    by = cuda.blockIdx.y   # ordonnée de 0 à 31 du bloc dans la grille
    
    # Block width, i.e. number of threads per block
    bw = cuda.blockDim.x  # largeur du bloc : nombre de threads en colonnes dans le bloc
    bh = cuda.blockDim.y  # longueur du bloc : nombre de threads en lignes dans le bloc

    gw = cuda.gridDim.x
    gh = cuda.gridDim.y
    
    step_x = bw * gw
    step_y = bh * gh

    start_x = x = tx + bx * bw 
    start_y = ty + by * bh
    
    for x in range(start_x, width, step_x):  # Il parcourt les colonnes de l'image avec x
        real = xmin + x*pixel_size_x  # Puis il calcule real en fonction de l'abscisse x dans l'image
        for y in range(start_y, height, step_y):  # Pour chaque colonne il parcourt les lignes
            imag = ymin + y*pixel_size_y  # Puis il calcule imag en fonction de l'ordonnée y dans l'image
            color = mandel(real, imag, iters)  # et appelle mandel pour chaque pixel avec real et imag
            image[y, x]  = color

import matplotlib.pyplot as plt
gimage = np.zeros((1024+1, 1536+1), dtype=np.uint8)
blockdim = (8, 8)
griddim = (72, 4)  # la grille utilise les colonnes en 1ere coordonnée
xmin, xmax, ymin, ymax = np.array([-2.0, 1.0, -1.0, 1.0]).astype('float32')
iters = 50

start = timer()
d_image = cuda.to_device(gimage)
create_fractal[griddim, blockdim](xmin, xmax, ymin, ymax, d_image, iters)
gimage = d_image.copy_to_host()
dt = timer() - start

print("Mandelbrot created on GPU in %f s" % dt)
plt.imshow(gimage, cmap='jet');  

Bien­ve­nue au pays des déve­lop­peurs Python sur GPU !

Pour aller plus loin

Il existe de nombreux tuto­riaux et livres sur le calcul pour GPU avec Python.

Les articles du compte GitHub de Jean François Puget consti­tuent d’ex­cel­lentes lectures :

• How To Quickly Compute The Mandel­brot Set In Python
• How To Quickly Compute Julia Set In Python

Deux livres inté­res­sants sur les GPU :

Hands-On GPU Compu­ting with Python

Source Packt­Pub Auteur : Avima­nyu Bandyo­padhyay

En quelques mots :

• Il prend le temps de présen­ter l’état de l’art de la disci­pline et les appli­ca­tions indus­trielles
• Il vous aide à choi­sir une solu­tion maté­rielle
• Il présente bien les archi­tec­tures NVIDIA et AMD
• De nombreuses librai­ries sont abor­dées
• Enfin, il a été publié en mai 2019, il reste à jour
• Il est un peu juste si vous souhai­tez creu­sez le sujet de la program­ma­tion GPU

Hands-On GPU Program­ming with Python and CUDA

Source Packt­Pub Auteur : Tuoma­nen

En quelques mots :

• Il est spéci­fique à NVIDIA mais va bien plus loin dans la program­ma­tion CUDA
• Il reste majo­ri­tai­re­ment foca­lisé sur PyCUDA, donc il y aura aussi du code en C : mais c’est ce qu’il annonce
• Il propose pas mal d’exer­cices pratiques

Licence

Ce tuto­riel et les images qu’il a géné­rées sont sous licence : CC BY-NC-SA 4.0

Vous pouvez copier, modi­fier et distri­buer ce tuto­riel sous réserve des condi­tions de la licence, dont :

• Respec­ter le crédit de l’au­teur : Gaël Pegliasco
• Respec­ter le crédit des images externes au cours ayant permis de l’illus­trer qui possèdent leur propre licence
• Ne pas l’uti­li­ser dans un but commer­cial
• Parta­ger vos adapa­ta­tions sous la même licence

Il est acces­sible sous forme de Note­book Jupy­ter sous GitHub à cette url : https://github.com/Mordi­cu­sEt­Cu­bi­tus/Cours­Py­thon/tree/master/gpu

En savoir plus

• Article Calcu­­lez sur GPU avec Python – Partie 1/3
• Article Calcu­­lez sur GPU avec Python – Partie 2/3
• Décou­vrez toutes nos forma­tions IA / Data Science
• Notre exper­tise IA / Data Science