Définition et constitution des bureaux de vote

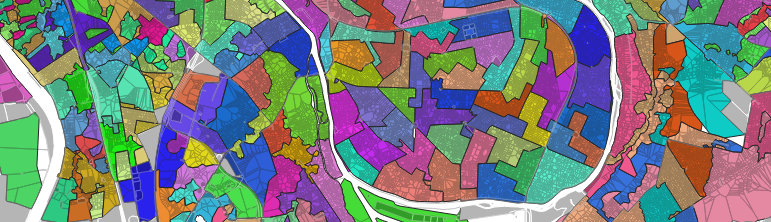
La représentation des résultats des élections par bureau de vote sur une carte n’est pas une chose courante, car en effet cela n’est pas aisé. Nous allons donc voir ici une approche pour produire des géométries intelligibles à partir des données des listes électorales qui se voudraient disponibles.

Lors des élections, les électeurs sont appelés à voter dans des bureaux de vote qui leur sont désignés. Chaque bureau possède une urne et une limite du nombre d’électeurs. Un lieu physique, comme une mairie ou une école, peut regrouper plusieurs bureaux de vote. La définition du bureau de vote, qui nous intéresse ici, est celle stipulant qu'une liste d'électeurs y est rattachée.

Cette affectation est déterminée par la mairie de chaque commune. Il s’agit en fait de rattacher des adresses à des bureaux de vote et non les électeurs eux-mêmes. Cette répartition par adresse dans les communes est publiée par des arrêtés préfectoraux.

Les communes utilisent différentes approches pour regrouper les adresses en bureau de vote. Nous pouvons notamment le voir dans l’exemple de l’arrêté préfectoral de la Gironde à compter du premier janvier 2020.

• Les plus petites communes nécessitent qu’un seul bureau de vote, la définition se limite à « toute la commune ».
• Certaines communes un peu plus grandes peuvent utiliser des listes de bourgs ou lieux-dits : « électeurs domiciliés à Villagrains », « électeurs domiciliés sur le reste de la commune ». Nous pouvons encore trouver « Le Montaut - Maubuisson et son ancienne ZAC - Bombannes - Carcans-plage ».

Les communes les plus grandes requièrent un découpage du tissu urbain qui se base sur les rues et d'autres repères. Deux grandes approches sont utilisées.

• Définir des zones en suivant la voirie :

« le boulevard de la République du numéro 268 à la fin, l’avenue d’Arès, la limite de l’avenue Jean-Marcel Despagne jusqu’au n°85 et l’avenue des Hères ».

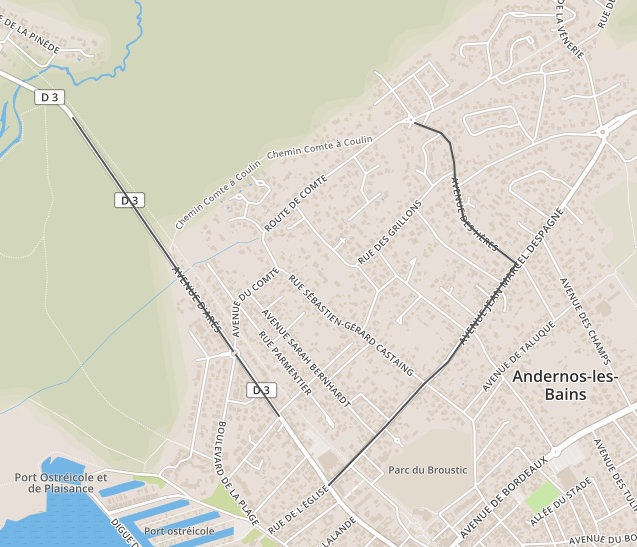
Représentation des délimitations de l’arrêté sur une carte. Nous observons que ce n’est ni complet, ni fermé.

« Allée de Charenton, allée de la Pinède, allée Saint Brice, allée des Amandiers, allée des Aulnes, allée des Bouleaux, allée des Bruyères, allée des Cigales, allée des Ecureuils, allée des Fougères, allée des Frênes, allée du Courlis, allée des Arbousiers, allée des Eglantiers, allée des Mûriers, allée des Oliviers, allée du Bois d’Armand, allée du Domaine des Lugées, avenue de la Libération, avenue de la Meule, avenue des Tamaris, boulevard de l’Aérium, boulevard Javal, impasse de Charenton, impasse des Brandes, impasse des Cigales, impasse des Eucalyptus, impasse des Genêts, impasse des Grillons, impasse du Ruisseau, impasse Saint Brice, lot Le Bois d’Armand, lot. Les Mimosas, résidence Les Cascades de Saint Brice, rond Point Saint-Brice, rond Point des Lugées, rond Point Lamartine, rue Albert Morange, rue André Labrunette, rue Chéri Ducamin, rue Damien Barrau, rue de la Chêneraie, rue des Ajoncs, rue des Chrysalides, rue des Cigales, rue des Criquets, rue des Grépins, rue des Mimosas, rue des Ormes, rue des Oyats, rue du Cirès, rue du XIV Juillet, rue Lamartine, rue Paul Verlaine, rue Ronsard, rue Victor Hugo, allée des Pinsons, avenue des Tourterelles, résidence du Parc, cité du Paradis, cité Matin Clair et rue des Fauvettes »

• Lister des adresses, toutes les adresses d’une voie ou seulement des sections :

« Avenue Jules Ferry (du 2 au 40 – du 1 au 99 et du 46 au 1000), rue Jean Prat, place du 19 mars 1962, rue Nelson Mandela, lieu dit « Jean Prat » lotissement COGEDIM, impasse du Hameau de Jean Prat, lieu dit « Carteau », rue Vivaldi, impasse des 4 Saisons et lotissement « les 4 Saisons », rue Django Reinhardt, rue Boris Vian et rue Coluche »

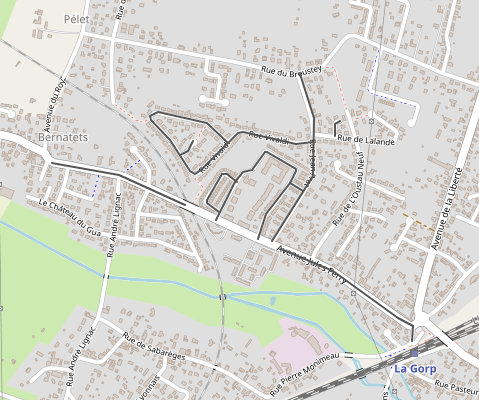
Représentation des tronçons de voies concernés. Nous observons qu’ils ne sont pas connexes.

« Rue de Barbère, chemin de l’Oeil du Pas, rue Alfred de Musset, rue de Canteranne, chemin de Napoléon, rue du Chêne vert, rue du Chêne vert prolongée, avenue de la Libération, rue de la Gare, rue Roger Salengro, rue Simone Signoret, rue Jacqueline Auriol, chemin du Moulin, impasse de la Libération, rue du Maréchal Foch, rue du Maréchal Foch prolongée, place de la Libération, rue de la Vierge, rue Victor Hugo (du 31 au 55 et du 32 au 56), rue de la commanderie des Templiers, rue de Chauvet, avenue de St Loubès, chemin de la Ricodonne, rue Max Linder, rue de Chante Alouette, chemin de la Hourcade, rue de Beauséjour, rue de Brandier, rue de la Croix noire, rue de Malleret, impasse du Maréchal Foch, rue Emile Larrieu, lieu dit « la Croix noire », lieu dit « l’Oeil du pas », lieu dit « le Poteau », lieu dit « la Ricodonne », lieu dit « Chante Alouette », lieu dit Beauséjour, lieu dit « Brandier », lieu dit « Chauvet », lieu dit « la Hourcade », lieu dit « le Chêne vert » et lieu dit « le Gaes ». »

Les électeurs et les adresses rattachées aux bureaux de vote sont centralisés par l’INSEE à l’aide du logiciel dédié à cet usage « Élire ».

Attention, il faut noter que la définition des bureaux de vote n’est pas la même chose que le découpage électoral. Ce dernier est l’affectation des bureaux de vote à des circonscriptions électorales.

De la représentation des bureaux de vote

Les définitions de bureaux de vote peuvent ne pas être initiées par des sectorisations géographiques. Leurs représentations sur une carte ne sont donc pas forcément évidentes. Il s'agit d'un problème similaire à celui des codes postaux, que l’on aime également s’imaginer comme de simples polygones regroupant ou découpant des communes. En réalité, ces derniers sont eux aussi des regroupements d’adresses.

Les définitions peuvent être basées sur des blocs de maisons ou des parties de blocs de maisons. Mais elles peuvent alternativement reposer sur des groupes d’adresses de rues verticales pour un bureau et horizontales pour un autre, c'est pourquoi ce tissage est difficile à représenter. D’autant plus que les rues françaises sont rarement toutes verticales et horizontales. Il existe même des communes où les électeurs sont répartis de façon alphabétique : la représentation graphique n’aurait alors rien à envier à l’esthétique une belle salade de fruits.

Avant même de traiter de l’aspect que nous attendons de cette représentation, il est nécessaire de se pencher sur l’obtention des données.

Certaines communes utilisent un découpage géographique comme base de construction des bureaux et le diffusent notamment en OpenData. Néanmoins cela reste limité à quelques grandes villes.

Une autre solution est d’utiliser le contenu des arrêtés préfectoraux pour reconstituer ces aires. Cependant, il ne s’agit que de réaliser une interprétation. Si l’on peut espérer pouvoir suivre le découpage en fonction de la voirie, il n’est pas toujours évident de découper les blocs de maisons ou encore de savoir où sont les limites de lieux-dits, dont la définition n’est pas connue, par exemple avec « Maubuisson et son ancienne ZAC ». Cette approche est celle réalisée par le projet universitaire « Cartelec » qui l’a mis en place pour quelques années et grandes villes. La réalisation de ce travail pour l’ensemble du territoire à chaque mise à jour représenterait une charge de travail conséquente.

La dernière solution est de repartir des listes électorales, c’est-à-dire des listes d’adresses rattachées aux bureaux de vote pour en reconstituer leurs périmètres géographiques. En 2015, Joël Gombin a exploré cette méthode dans son article « Créer et diffuser de l’information électorale au niveau des bureaux de vote ». C’est cette approche qui nous sert de base et que nous cherchons à étendre ici.

Reconstituer les géométries des bureaux de vote depuis les listes électorales, approche précédente

Cette méthode consiste tout d’abord à obtenir les listes électorales. Il est théoriquement possible à tout électeur de demander les listes électorales, à condition de ne pas en faire un usage commercial. En 2015, il fallait les demander aux mairies de chaque commune. En 2020, c’est théoriquement plus simple puisqu'il faut adresser les demandes aux préfectures pour un département entier.

Ensuite, il est nécessaire de convertir ces adresses en coordonnées géographiques pour les placer sur une carte, c’est le géocodage. Toutefois le géocodage n’est pas un processus parfait, ainsi il peut en résulter des erreurs ou des inexactitudes.

L’étape suivante consiste à passer d’adresses ponctuelles à des surfaces. Pour cela on utilise un diagramme de Voronoï qui dessine autour de chaque point adresse une cellule qui représente la portion du territoire qui est plus proche de cette adresse que des autres.

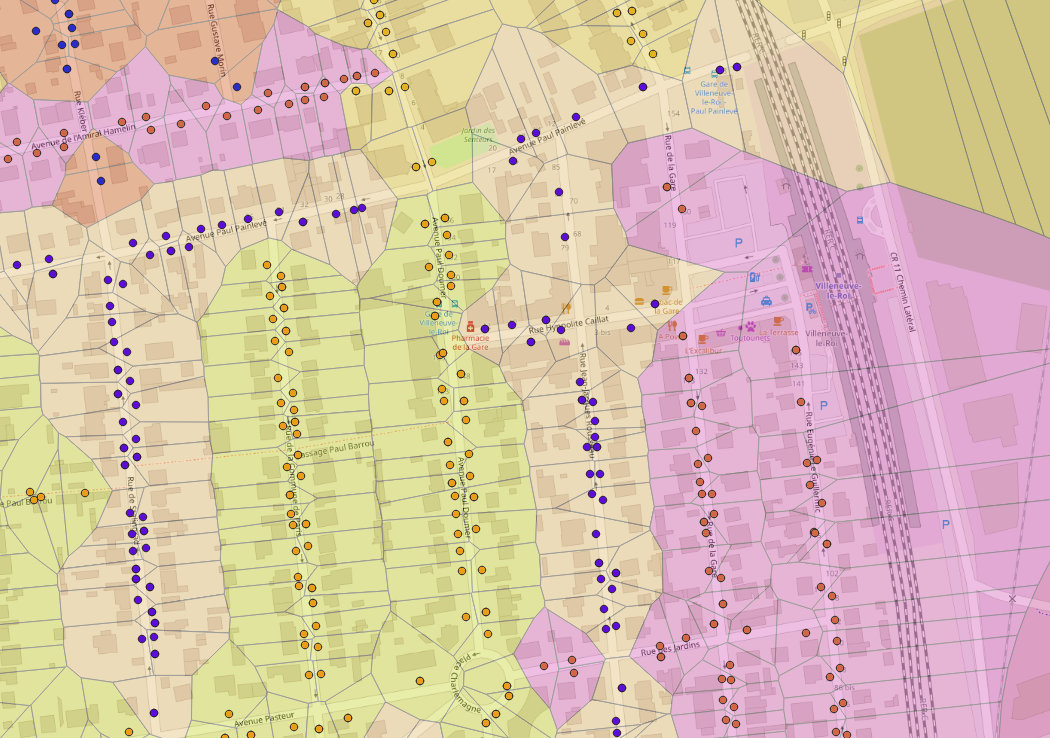
Cellules de Voronoï pour chaque adresse. Couleur par bureau de vote.

Pour finir, les cellules sont regroupées par bureau de vote pour obtenir une géométrie associée.

En théorie l’accès aux listes électorales est possible, mais en pratique il n’y a souvent pas de retour et il arrive qu'il ait de l’obstruction pour ne pas les communiquer. De ce fait, la récupération de l’ensemble des listes électorales de France parait peu réaliste.

L’autre inconvénient de cette méthode est l’aspect très rugueux des contours des bureaux de vote produits, alors qu’ils sont initialement basés sur la voirie à l’aspect beaucoup plus linéaire. C’est ce dernier point que nous cherchons à améliorer ici.

Reconstituer les géométries des bureaux avec Voronoï sous contrainte de la voirie

L’idée générale est la même que celle précédemment détaillée. Nous faisons intervenir la géométrie de la voirie pour limiter et guider la construction des géométries.

Pour la suite, nous allons charger les données, puis effectuer les calculs dans une base de données PostgreSQL avec l’extension spatiale PostGIS.

Obtenir les adresses rattachées aux bureaux de vote

Étant donné que l’INSEE détient l’ensemble des listes électorales, nous avons commencé par leur demander à avoir accès à ces informations. Nous avons demandé les adresses des électeurs ainsi que le bureau de rattachement de chaque adresse. Les informations personnelles, comme les noms ou les dates de naissances, n'ont pas été demandées. L’INSEE a rejeté notre demande pour raison juridique.

La voie naturelle pour obtenir ces information est de les demander aux préfectures, ce que nous avons fait. Malheureusement, nous n’avons pas eu de retours des cinq préfectures à qui nous nous sommes adressés.

Comme solution de repli, un jeu de données disponible sur Internet et diffusé dans le cadre du « DataCamp CadElect » de 2016 a été utilisé : les adresses par bureau de vote du Val-de-Marne.

Géocodage

Les listes d’adresses associées aux bureaux de vote ne sont que des adresses sous forme textuelle. Elles doivent être converties en coordonnées géographiques avant de pouvoir être utilisées. Nous utilisons un fichier d’adresses de 2016 qui a été géocodé en 2016. Nous aurions voulu pouvoir géocoder à nouveau ce fichier pour essayer d’améliorer la qualité du résultat. Toutefois cela nécessite d’avoir une base d’adresses dans le géocodeur du même millésime que les données. Nous nous satisferons donc du travail de géocodage déjà effectué.

Il a été réalisé avec la Base Adresse Nationale (BAN) et le géocodeur Addok. Le résultat du géocodage comporte non seulement des coordonnées, latitude et longitude pour chaque adresse, mais également deux indicateurs de qualité indépendants entre eux :

• un score entre 0 et 1,
• un niveau de détail du résultat, à la ville, à la rue, à l’adresse, au lieux-dit.

Nous voulons travailler au niveau de l’adresse de chaque électeur, il est donc important pour la suite d’avoir une bonne confiance dans le résultat du géocodage (score) et une bonne précision (niveau de détail). Afin de réduire le bruit dans les données pour la suite de nos calculs, nous ne retenons donc que les résultats du géocodage avec un niveau de détail « à l’adresse » ou « au lieux-dit » et dont le score est supérieur à 0,7. Ce filtrage nous fait écarter 3 000 adresses sur un total de 150 000, soit 2 %.

Bien que notre fichier d’adresses ne contenait pas d’adresses en doublon, le géocodage a pu produire des coordonnées au même emplacement. Nous dédoublons donc les coordonnées géographiques pour ne retenir qu’un bureau de vote par coordonnée. Pour chaque coordonnée, nous ne gardons que le bureau de vote le plus représenté. Cette déduplication réduit de 6 % le nombre de points à traiter.

Pour terminer, nous ne retenons pas les points géocodés trop fortement à l’écart d’un même bureau de vote pour compenser l’effet de mauvais géocodage qui aurait passé les filtres précédents. En effet, nous nous attendons à ce que les points d’un même bureau de vote soient réunis. Pour chaque bureau de vote, nous calculons une médiane géométrique de l’ensemble de ces points. Il s’agit d’une sorte de centroïde mais moins sensible aux valeurs les plus écartées ST_GeometricMedian(). Ensuite, nous calculons la distance médiane de l’ensemble des points du bureau de vote à ce point central (point médian) et écartons les points de distance extrême, 5 fois supérieures à la distance médiane, cela représente moins de 0,3 % des points.

Limites de communes

Nous avons besoin de travailler par commune, les bureaux de vote sont les découpages des communes. Nous utilisons donc le découpage des communes de 2016 issu d’OpenStreetMap pour être en cohérence avec le millésime de notre liste d’adresses d’électeurs.

Voirie et blocs de maisons

La voirie est obtenue depuis les données d’OpenStreetMap. Des exports par département sont mis à disposition par OpenStreetMap-France. À l’aide du logiciel imposm nous pouvons configurer n'importe quel type d’objets que nous souhaitons filtrer et importer dans une base de données.

Dans notre cas, nous allons utiliser tout ce qui sert de démarcation sur le territoire : toute la voirie dont les routes et les rues, les voies ferrées, les cours d’eau, les berges et canaux. Nous excluons tout ce qui est en sous sol (tunnels de plus de 100 m), mais conservons les ponts.

Tous ces tracés sont réunis pour servir de ligne de découpage aux polygones des communes. Pour cela, la fonction ST_Split() de PostGIS est utilisée.

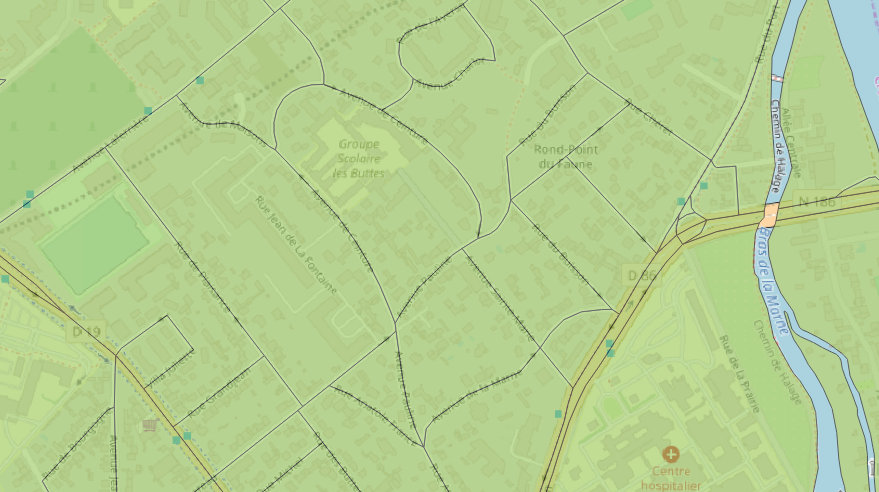
Découpage par blocs en suivant la voirie et les cours d’eau. Seules les voies délimitant un périmètre sont utilisées.

L’idée générale est d’obtenir des blocs de maisons, mais nous obtenons plus de blocs que cela. Par exemple, l’intérieur des giratoires est découpé ainsi que les parcs ou encore l’espace entre les voies à chaussées séparées.

Tous les blocs découpés ne contiennent donc pas forcément d’adresses et ne pourront pas être associés directement un bureau de vote.

L’utilisation de l’intégralité de ces lignes de démarcation conduirait par endroit à un sur-découpage totalement artificiel qui ne correspond pas à l’objet de notre traitement. Il convient de ne pas utiliser les « voies de service » routières comme ferrées. Un bloc entre deux voies ferrées dans une gare de triage n’a vraiment pas d’intérêt pour le découpage des bureaux de vote. De plus, nous retirons également des polygones des communes le lit des cours d’eau et autres éléments surfaciques hydrographiques.

Cette approche par blocs a deux défauts: Comme nous venons de le voir, ces blocs ne sont pas tous associables à des adresses d’électeurs. D’autre part, certains blocs ont des géométries très effilées comme le long des cours d’eau, des voies ferrées ou des autoroutes, pouvant se poursuivre sur des kilomètres sans être interrompus.

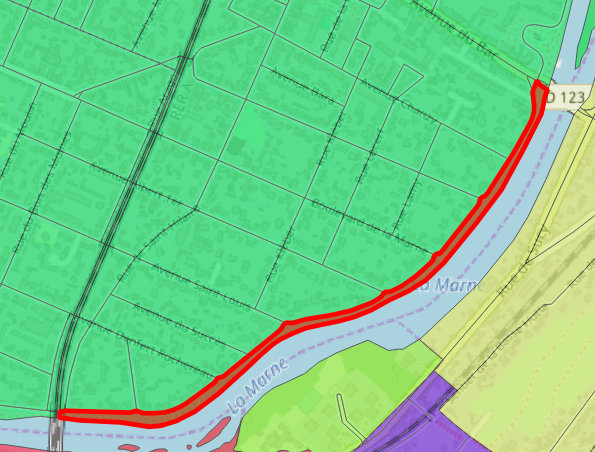
Bloc surligné en rouge de forme très allongé sur les berges.

Diagramme de Voronoï sous contrainte

Comme nous l’avons vu ci-dessus, un diagramme de Voronoï permet de découper le territoire autour de chaque adresse en posant des limites équidistantes avec les autres points adresses environnantes.

Nous souhaitons créer et limiter ces diagrammes de Voronoï aux blocs de maisons afin que les limites de bureaux suivent la voirie. La première étape consiste donc à regrouper les adresses par bloc. Nous lions les points adresses aux blocs s’ils sont à l’intérieur de ces blocs. Pour cela, la fonction ST_Intersects() de PostGIS est utilisée. Nous allons ensuite calculer le découpage de Voronoï pour les points d’un bloc avec la fonction homonyme de PostGIS : ST_VoronoiPolygons().

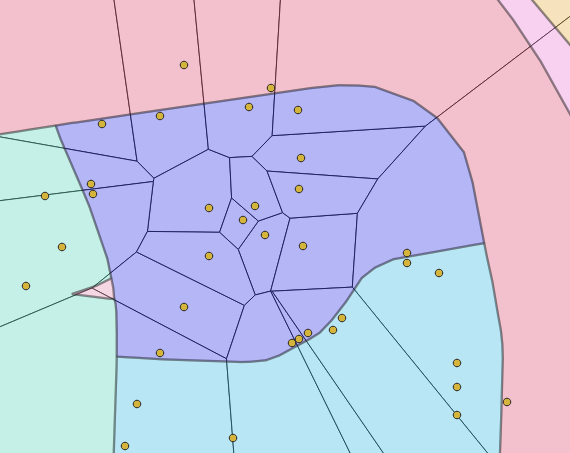
Diagramme de Voronoï pour le bloc bleu central. Seuls les points de ce bloc servent de base pour le calcul des cellules.

Par définition, un diagramme de Voronoï n’est pas borné pour les cellules périphériques. PostGIS le borne tout même à une zone de référence pour ne produire que des « polygones fermés ». Afin d'éviter les erreurs d’arrondis et de calculs géométriques, nous réaliserons l'intersection entre les cellules et le bloc de référence plus tard.

Chaque adresse est associée à un bureau de vote, il en est donc de même pour chaque cellule. Si la stratégie de définition des bureaux par la commune est d’utiliser des blocs, la totalité des cellules d’un bloc devraient être associée à un seul bureau. Mais, il arrive souvent pour diverses raisons que plusieurs bureaux soient présents dans un même bloc.

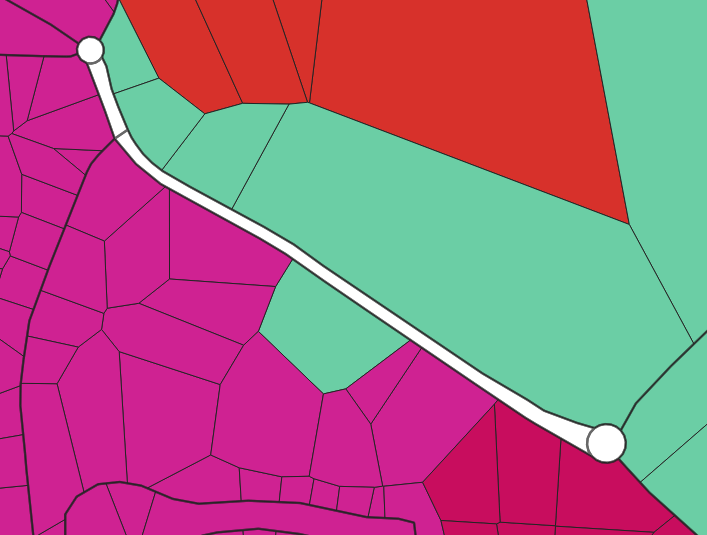
Cellule isolée dans un bloc. Couleur par bureau de vote. Les traits plus épais délimitent les blocs.

Nous pouvons trouver au sein d’un bloc des cellules isolées, c’est-à-dire qu’elles ne jouxtent pas d’autres cellules du même bureau de vote. Si nous identifions de telles cellules qui ont plusieurs voisines et dont toutes ses voisines ont toutes un autre et même bureau de vote, alors nous la mutons vers ce même bureau de vote. Nous considérons que ce cas est une anomalie. Elle peut résulter d’un mauvais géocodage ou d’un mauvais alignement entre la position de l’adresse géocodée et la voirie d’OpenStreetMap, faisant ainsi passer le point de l’autre côté de la voie.

Malgré tout, ces cellules isolées peuvent résulter d’associations intentionnelles à un bureau de vote non connexe. Par exemple : en mettant dans un autre bureau de vote un immeuble ou une résidence avec une population importante afin d'ajuster l’équilibrage du nombre d’électeurs. Nous pouvons également trouver des anomalies de numération réelles sur le terrain : par exemple un numéro pair se trouvant du côté impair. Toutefois, la mutation de ces cellules isolées permet tout de même d’obtenir des géométries mieux alignées sur la voirie et donc plus lisibles.

Réassembler par bureau de vote

Après la mutation des cellules isolées nous allons pouvoir faire l’union des cellules d’un même bureau de vote.

Tout d’abord, si toutes les cellules d’un bloc sont du même bureau de vote, nous utilisons directement la géométrie du bloc. Cela nous évite d’avoir à faire l’union des cellules de ce bloc, mais surtout d’introduite de possibles erreurs d’arrondi et de géométrie par l’union de nombreux petits polygones.

Nous réaliserons cependant l’union des cellules dans les autres cas. Celle-ci se fait à la fois par bureau de vote et par bloc en utilisant la fonction ST_Union(). Comme nous l’avons vu plus haut les cellules extérieures du digramme de Voronoï ne sont pas bornées. Il va donc en être de même pour l’union des cellules. C’est donc maintenant que nous limitons cette union à la géométrie des blocs, nous les découpons donc avec ST_Intersection(). Nous procédons ensuite à l’union de l’ensemble des parties des bureaux de vote.

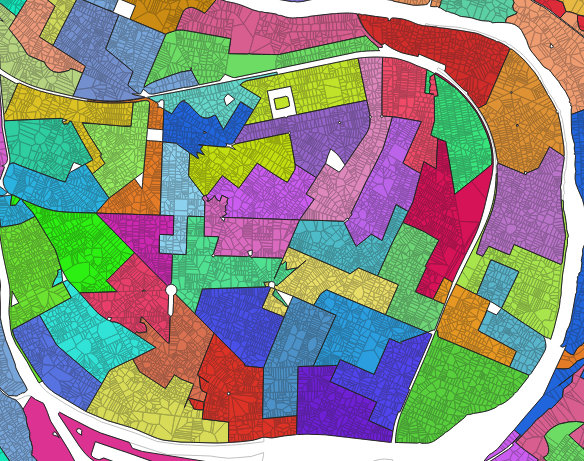
Résultat de l’union de cellules basées sur un découpage des bureaux de vote par blocs.

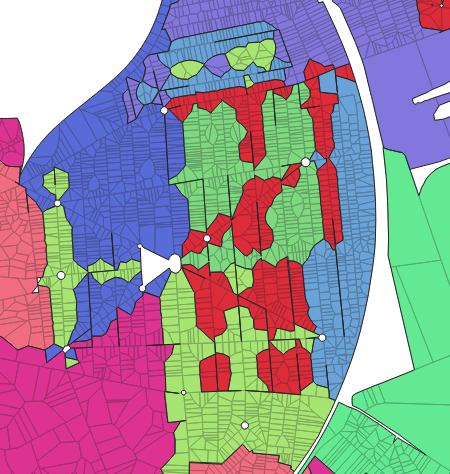
Résultat de l’union de cellules basées sur un découpage des bureaux de vote par adresse.

Nous choisissons également de limiter la géométrie des bureaux de vote à 400 m à la ronde de l'emplacement des adresses de ces mêmes bureaux. Nous faisons cela avec un objectif double. D’une part limiter les blocs effilés (bord de cours d’eau, de voies ferrées…). D’autre part de ne pas inclure de larges espaces comme des champs, des forêts ou encore des aéroports dans les aires des bureaux de vote, cela afin de ne pas les surdimensionner par rapport au nombre d'électeurs.

L’approche consistant à limiter les cellules de Voronoï aux blocs permet d’obtenir des contours de bureau de vote plus lisses. Toutefois, elle introduit également des trous car certains blocs ne sont pas associés à des adresses.

Joindre et simplifier les géométries des bureaux de vote

Pour la suite, nous allons chercher à combler les trous entre les géométries des bureaux de vote pour obtenir des formes plus naturelles et lisibles en essayant de rester dans l’esprit du découpage suivant la voirie quand cela à du sens.

Les blocs libres d’adresses sont souvent petits et enchevêtrés entre les voies, giratoires, carrefours complexes ou de tailles plus importantes : places, parkings, parcs, centres commerciaux non habités…

Nous cherchons à les agréger aux polygones des bureaux de vote que nous avons déjà constitués. Ces blocs libres sont par nature alignés avec la voirie qui a permis de les définir. Cependant, certains blocs non libres d’adresses ont été découpés entre plusieurs bureaux et ont donc engendrés de nouvelles délimitations non associées à la voirie. Les blocs libres jouxtant ces nouveaux découpages ne vont donc pas être alignés.

Il est nécessaire de découper les blocs libres par les prolongements des découpes internes des blocs divisés en plusieurs bureaux de vote. Nous passons ici sous silence les calculs nécessaires à l’identification et la prolongation des frontières internes aux blocs. Mais l’objectif est d’appliquer à nouveau ST_Split() aux blocs libres pour les découper suivant ces nouvelles limites.

Découpes supplémentaires des blocs libres.

Il faut ensuite établir la stratégie d’agrégation des blocs libres aux bureaux de vote. Quel est le critère qui fait qu’unir un bloc libre à la géométrie d’un bureau de vote va rendre cette dernière plus naturelle ? Comment choisir le bureau de vote quand un bloc libre en jouxte plusieurs ? Intuitivement nous voulons des bureaux de vote plus carrés et alignés entre eux sur les axes principaux.

Nous avons voulu maintenir une solution simple, sans investir dans des stratégies complexes. Nous avons toutefois dû tester de façon empirique pour déterminer des critères d’agrégation. Tout d’abord, nous utilisons une approche « gloutonne », c’est-à-dire qu’une fois que nous choisissons d’affecter un bloc libre à un contour de bureau de vote nous ne revenons pas en arrière. Nous posons également la contrainte d’acceptabilité suivante :

• Le bloc libre peut être agrégé s’il est situé dans une zone à moins de 150 m de la géométrie initiale du bureau de vote.

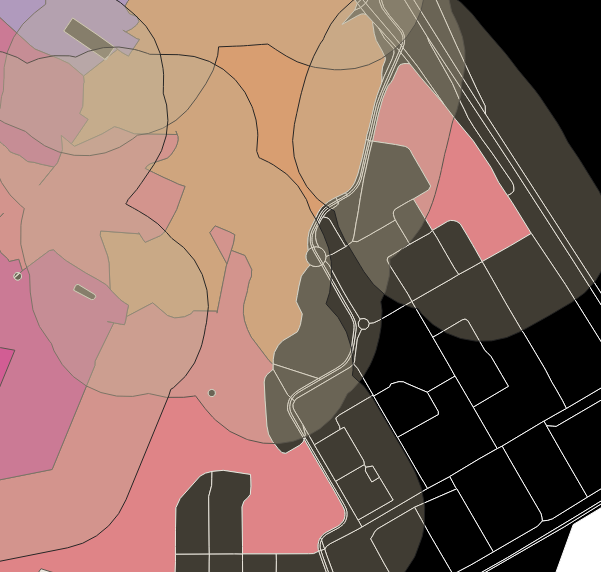
Zone tampon au tour des bureaux de vote pour limiter l’agrégation de blocs libres.

Nous itérons en agrégeant les blocs libres de manière gloutonne. À chaque itération, nous repartons de la nouvelle géométrie agrégée des bureaux de vote pour déterminer les futurs blocs libres qui peuvent être pris en compte. Nous avons ainsi une croissance des géométries des bureaux de vote. Nous rajoutons alors la condition suivante :

• Un bloc libre peut être agrégé s’il jouxte le bureau de vote par plus d’un sommet.

Nous prenons ensuite les blocs libres qui répondent le mieux aux critères suivant, et dans cet ordre :

1 Le bloc libre permet de joindre des parties non connexes d’un même bureau de vote. Le bloc va au bureau de vote dont le nombre de composantes après union est le plus faible.

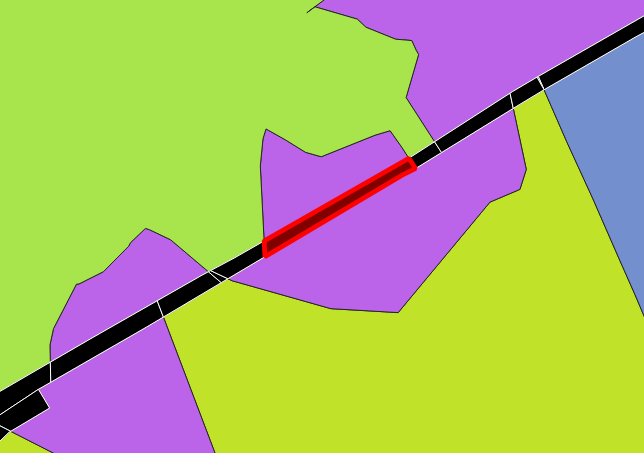
Mise en surbrillance d’un bloc libre faisant la jonction entre deux composantes d’un même bureau de vote.

2 La géométrie simplifiée du bureau de vote après union avec le bloc libre contient moins de sommets qu’avant. Le bloc va au bureau dont la réduction du nombre de sommets (avant / après) est la plus grande.

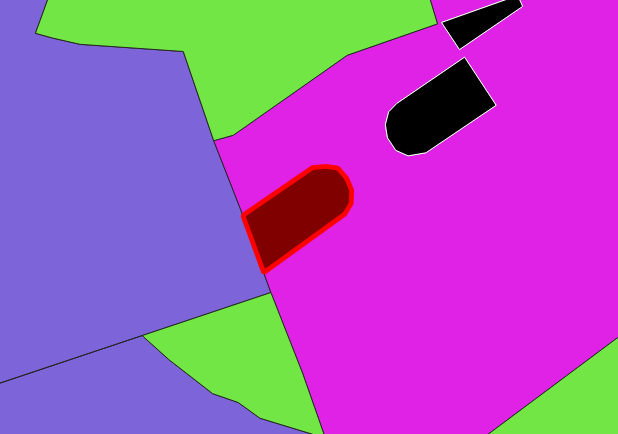
Mise en surbrillance d’un bloc libre permettant ainsi de simplifier la forme du bureau de vote à sa droite.

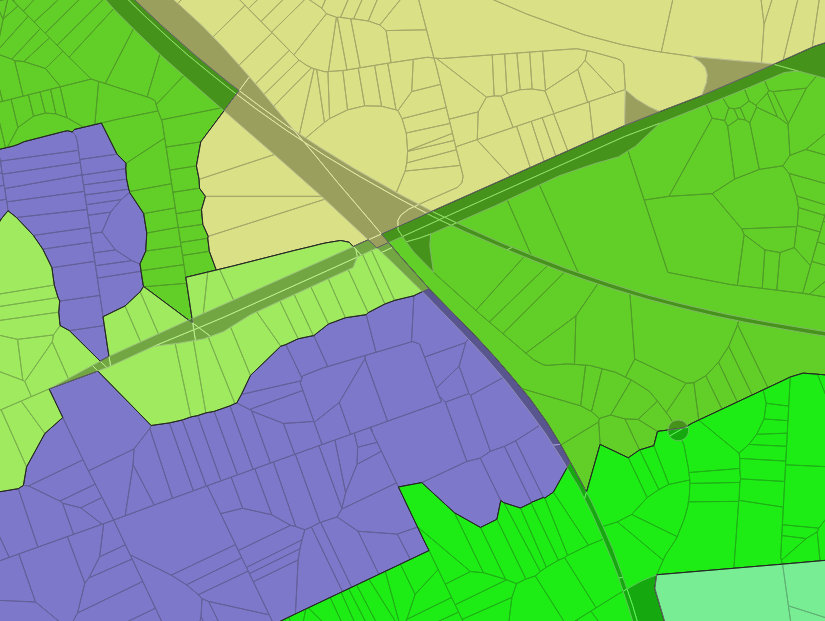
Résultat de l’agrégation des bureaux de vote avec les blocs libres. Une couleur par bureau de vote. Les blocs plus foncés sont les blocs initialement libres d’adresse.

Simplification

Les géométries des bureaux de vote obtenues peuvent être simplifiées. Il faut bien sûr les simplifier de façon topologique et non polygone par polygone. Ce sont les limites des géométries entre bureaux de vote qu’il faut simplifier. Il y a en particulier deux types de limites.

• Celles obtenues en suivant un découpage linéaire de la voirie.
• Celles découpant des blocs, résultat de l’union de cellules de Voronoï. Ces dernières ont toujours le même défaut d’aspect que la méthode de traitement initiale avait. La simplification va les adoucir mais au risque d’introduire des erreurs et en faisant passer un point adresse d’un bureau d’un vote à un autre.

Conclusion

L’approche proposée ici à l’aide de diagrammes de Voronoï limités aux blocs de maisons et par agrégation des blocs libres d’adresse permet d’obtenir un résultat visuellement satisfaisant.

Il est cependant difficile d’en mesureur la qualité à cause de la difficulté d’obtenir des données et d’avoir des bases de comparaison. La stratégie d’agrégation des blocs libres aux bureaux de vote mériterait d’être plus approfondie pour déterminer de meilleurs opérateurs d’agrégations et pour autoriser un retour arrière afin de réaffecter les blocs libres à un autre bureau de vote.

Toutefois, le travail réalisé ici permet d’obtenir de façon entièrement automatique des géométries « propres » pouvant permettre la réalisation de cartes de bureaux de vote.

Les données et codes sources utilisés pour ce projet sont disponibles sur Github : https://github.com/makinacorpus/bureaux-de-vote-reconstruction.

En savoir +

Pour l'événement des GéoDataDays à Montpellier le 16 septembre 2020, Makina Corpus interviendra en conférence sur la thématique suivante : "Élections : analyse spatiale et open data, une vision volontairement biaisée ? La carte : entre sensibilisation et manipulation."

Nos partenaires en parle…

L'AFIGÉO a relayé cet article dans son actu géomatique, en savoir plus.