Makina Blog
Deep clustering d'images aériennes
Cet article présente Deep Cluster, une méthode reposant sur l'utilisation conjointe d'un algorithme de clustering et d'un réseau de neurones (deep learning). Nous montrons que Deep Cluster réussit à grouper en ensembles cohérents des photographies aériennes récupérées via l'API Mapbox. Grâce à l'outil MLflow nous avons tracé et analysé les résultats obtenus par la méthode Deep Cluster. Dans cette publication nous donnerons quelques précisions sur l'utilisation de cet outil.
L'utilisation des techniques de Machine Learning afin de concevoir des outils intelligents pour les observatoires du paysage fait parti des problématiques de recherche et développement qui occupent nos équipes depuis plusieurs années. Nous nous intéressons notamment aux méthodes susceptibles d'organiser une base de données photographiques en groupes cohérents du point de vue perceptuel et sémantique. Dans ce contexte, la publication de Mathilde Caron et al. : Deep Clustering for Unsupervised Learning of Visual Features ne pouvait que retenir notre attention. Nous souhaitions savoir si cette méthode évaluée avec succès sur des photographies classiques, fonctionnerait également sur de la photographie aérienne.
Pourquoi s'intéresser à Deep Cluster ?
Dans le domaine de l'analyse d'images, les performances des réseaux de neurones sont spectaculaires, tant pour identifier le contenu d'une photographie que pour le localiser des objets d'intérêt. Néanmoins, comme l'illustre la figure 1, l'entraînement d'un réseau de neurones requiert la présence d'une vérité terrain. Concrètement, pour chaque image d'entraînement il nous faut un exemple de résultat attendu.
Le réseau de neurones analyse les données qui lui sont fournies et propose un classification de ces dernières. La vérité terrain permet de calculer l'erreur commise par le réseau de neurones, qui peut alors se mettre à jour pour produire une classification davantage pertinente. Le processus est répété jusqu'à ce que l'apprentissage ne s'accompagne plus d'une diminution de l'erreur commise.
Figure 1 : utilisation de la vérité terrain durant l'apprentissage d'un réseau de neurones.
Ainsi, si nous souhaitons entraîner un réseau de neurones à caractériser des types de paysages en fonction de photographies aériennes il est indispensable de créer un jeu de données où les images sont associées à un ou plusieurs types de paysages. La création de cette vérité terrain nécessite une expertise importante, pour concevoir une taxonomie de paysage pertinente comme pour associer chaque photographie aérienne à une ou plusieurs catégories de cette taxonomie.
Les méthodes d'apprentissage non-supervisé, comme illustré Figure 2, se libèrent de la contrainte de la vérité terrain. Pour ces méthodes la phase d'apprentissage consiste à analyser les propriétés des données les unes par rapport aux autres. Il peut s'agir de la distance entre les données, d'un calcul de densité ou de rechercher une les paramètres d'une loi de probabilité spécifique représentant au mieux les données. Les données d'apprentissage fournissent ainsi une base pour mieux comprendre les futures données.
Figure 2 : fonctionnement des algorithmes de clustering.
Dans cette catégorie de méthode, les algorithmes de clustering (en français « regroupement ») fournissent des solutions pour organiser les données en ensembles homogènes. Les groupes sont constitués durant les apprentissage, en associant les données similaires. Une fois l'apprentissage terminé, de nouvelles données peuvent être associées aux groupes ainsi créés.
Cependant utiliser un algorithme de clustering sur des photographies implique de décrire au préalable chaque image par un descripteur pertinent (généralement un vecteur numérique). Et justement, les réseaux de neurones constituent actuellement le moyen le plus efficace pour synthétiser le contenu d'une image en un descripteur adéquate, dans le cadre une problématique spécifique.
La méthode Deep Cluster s'appuie à la fois sur les avantages des méthodes d'apprentissage non-supervisé et sur ceux des réseaux de neurones :
- un réseau de neurones pré-entraîné produit les descripteurs pour les images ;
- ces descripteurs sont groupés à l'aide d'un algorithme de clustering ;
- les groupes de l'algorithme de clustering sont utilisés comme vérité terrain pour poursuivre l'apprentissage du réseau de neurones.
Le processus est répété plusieurs fois, créant un cercle vertueux : à mesure que le réseau de neurones s'entraîne, les descripteurs deviennent de plus en plus pertinents et plus ces descripteurs sont adaptés, plus les groupes formés par KMeans sont cohérents.
Adaptations réalisées par Makina Corpus
Nous avons testé Deep Cluster avec un ensemble de 8418 images aériennes couvrant en majeur partie le territoire de la France métropolitaine. Récoltées via l'API de Mapbox, ces photographies de 256 par 256 pixels correspondent à un niveau de zoom 12, ce qui nous permet de distinguer de manière assez précise différents type de paysages. Quatre exemples de photographies aériennes sont présentés Figure 3.
Figure 3 : 4 exemples d'images aériennes utilisées pour entraîner Deep Cluster.
Nous disposions 6313 images d’entraînement et 2105 images de test. Comme réseau de neurones nous avons choisi d'utiliser le modèle XCeption pré-entraîné sur Imagenet et fournit par la bibliothèque Keras. Ce réseau de neurones a l'avantage d'être relativement léger avec seulement 22 910 480 pondérations (là où ses concurrents VGG19 en comprend 143 667 240 et Resnet50 25 636 712) tout en obtenant pour le challenge Imagenet des résultats qui figurent parmi les meilleurs. Il constitue donc une amélioration par rapport aux réseaux de neurones testés par Matilde Caron et al.
Pour l'algorithme de clustering, nous avons utilisé l'implémentation de MiniBatchKMeans proposée par
Scikit-Learn. Bien qu'un peu moins précise que l'algorithme Kmeans, cette méthode passe mieux à l'échelle sur les jeux de données de taille importante, comme dans notre cas.
Contrairement à Mathilde Caron et al. nous n'avions aucune connaissance a priori sur le nombre de groupes. Nous avons privilégié un nombre de groupes faible (5) pour que chaque groupe puisse disposer de plusieurs centaines d'images. Nous nous assurons ainsi que le réseau de neurones n'est pas mis en difficulté par le nombre de données.
Il nous avons également pris en compte les déséquilibres qui peuvent apparaître en terme de nombre de données
attribués à un groupe. La fonction compute_class_weight de Scikit-Learn nous donne des pondérations pour chaque classe de manière à atténuer les disparités sur leur cardinalité.
Enfin nos tests comprenaient 10 itérations de l'algorithme DeepCluster.
Utilisation de MLflow
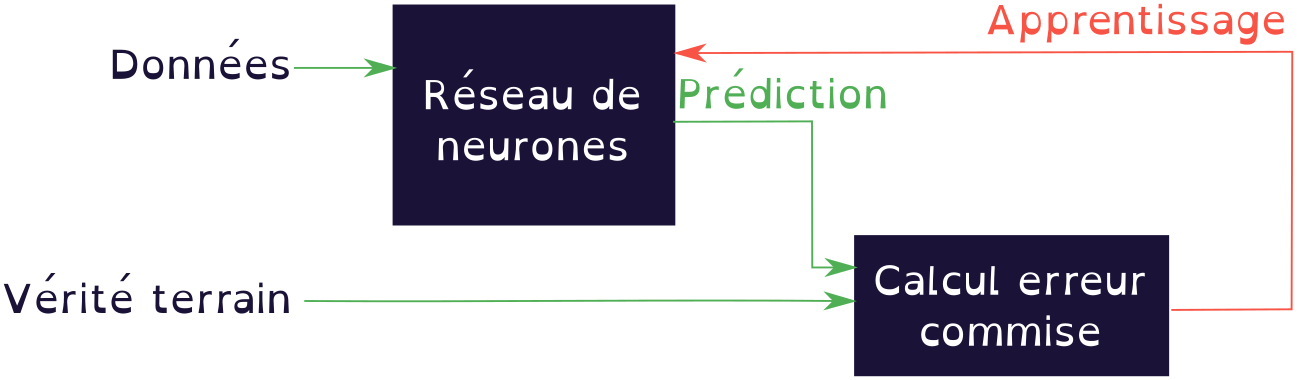
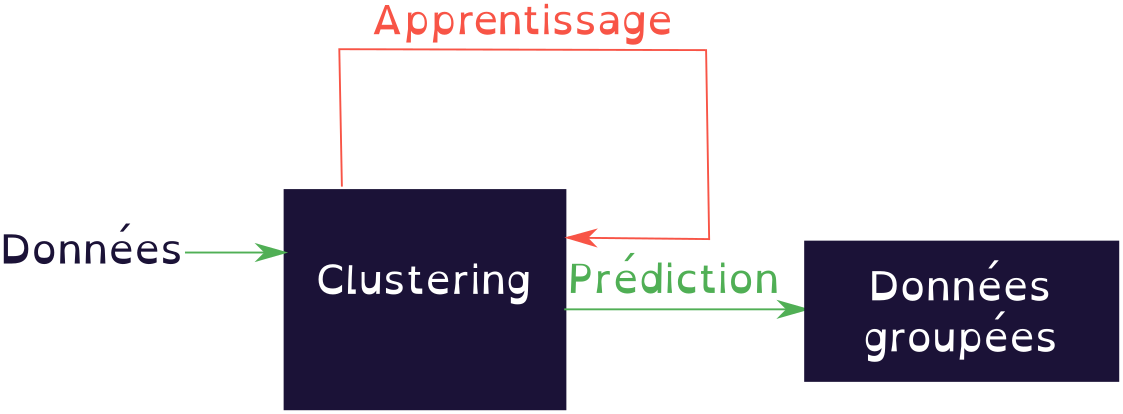
MLflow est un outil sous licence libre dont l'objectif est d’industrialiser de bout en bout les projets de Machine Learning, de la phase recherche à la mise en production. Actuellement nous étudions son intégration au sein de nos processus métiers.
MLflow se fixe deux objectifs :
- permettre la mise en production rapide et simple de modèles provenant de différentes bibliothèques (par exemple Scikit Learn et Tensorflow) ;
- permettre un suivi détaillé de la phase de design des modèles, facilitant notamment la reproductibilité des expériences menées.
C'est dans le cadre de cette deuxième problématique que nous l'avons utilisé, en nous limitant à ses fonctionnalités de tracking.
Après avoir importée la bibliothèque Python MLflow, nous lançons un **run** au niveau du point d'entrée principale de notre script Python :
with mlflow.start_run(): pass
Un run correspond généralement à une expérimentation menée. Dans notre cas il s'agit de l’entraînement de la méthode Deep Clustersur un ensemble de données. Lors d'un run, MLflow enregistre des paramètres et des métriques. Les paramètres sont des caractéristiques fixes de l'expérimentation. Dans notre cas nous avons par exemple :
with mlflow.start_run(): mlflow.log_params({ 'nb_clusters': args.nb_clusters, 'data_directory': args.data_directory, 'models_directory': args.models_directory, 'nb_steps': args.nb_steps })
Pour chaque expérimentation nous aurons donc accès au nombre de groupes demandés à l'algorithme de clustering, aux données utilisées, au répertoire où sont sauvegardés les réseaux de neurones obtenus après chaque itération et au nombre d'itérations réalisées par Deep Cluster. Nous pouvons ainsi facilement reproduire l'expérience.
Tout au long de l'expérimentation, grâce à MLflow, nous allons également enregistrer des métriques qui évoluerons au fil des itérations. Nous sauvegardons par exemple l'exactitude (accuracy) et le résultat de la fonction de coût (loss) obtenus par le réseau de neurones à la fin de chaque époque, et ce, pour les données d’entraînement comme pour celles d'évaluation.
mlflow.log_metrics({ 'train_loss': res_train[0], 'train_acc': res_train[1], 'ctrl_loss': res_ctrl[0], 'ctrl_acc': res_ctrl[1] })
MLflow fournit une application web facilitant la consultation des paramètres et métriques associés à chaque expérimentation. Elle se lance en ligne de commande :
mlflow ui
La figure 4 montre ce que nous obtenons après deux expérimentations :
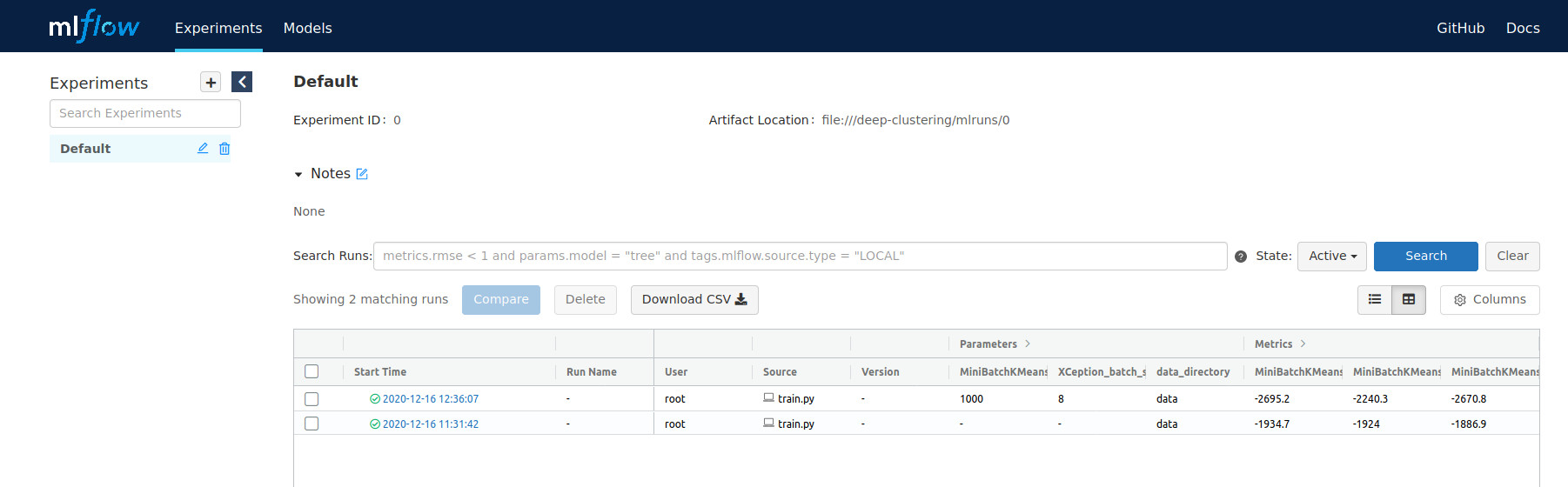
Figure 4 : interface de MLflow
Deux runs sont accessibles. Pour chacun d'entre eux, MLflow nous fournit les moyens de visualiser l'évolution d'une ou plusieurs métriques sur des graphiques adaptés.
Suivi de la progression de l'algorithme avec MLflow
Nous avons choisi de nous intéresser à trois types de métriques afin d'analyser la progression de DeepCluster durant l'entraînement :
- un score de performance pour la méthode de clustering : l'opposé des distances inter-groupes élevées au carré ;
- un score de performance pour le réseau de neurones : l'exactitude (en anglais accuracy) ;
- le nombre d'images associées à chaque groupe.
L'opposé des distances inter-groupes élevées au carré correspond à l'opposé de la distance moyenne entre le descripteur de chaque image et le centre du groupe auquel l'image est associée par l'algorithme de clustering. Il s'agit d'un score négatif qui tend vers 0 lorsque les groupes sont denses, i.e que les descripteurs forment un ensemble compact autour du centre du groupe. Comme l'amélioration du descripteur généré par le réseau de neurones permet à l'algorithme de clustering de produire des groupes plus homogènes, nous devrions voir ce score s'approcher de zéro tout au long des 10 étapes.
La figure 5 présente les résultats obtenus. Pour des raisons de capacités mémoires, les données ne sont pas présentées en un seul bloc à MiniBatchKMeans mais au travers de 7 lots contenant chacun un millier d'images.
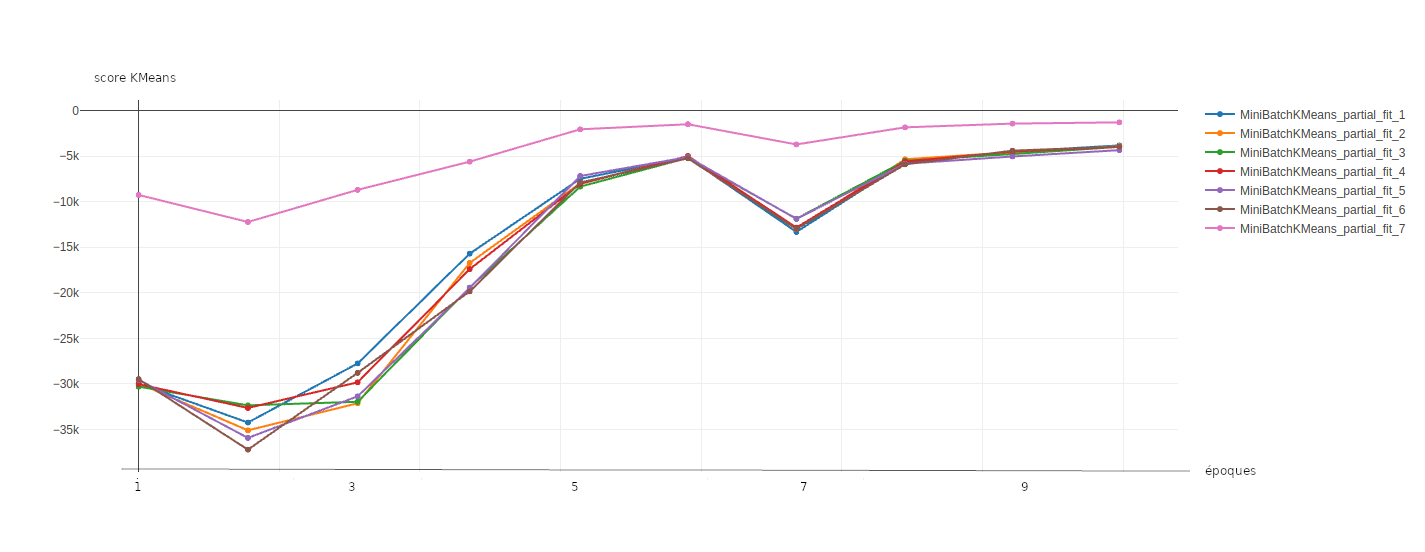
Figure 5 : évolution du score de l'algorithme MiniBatchKMeans sur les différents lots de données qui lui sont transmis.
Si les scores peuvent varier d'un lot à l'autre, tous suivent la même tendance. Durant les dernières étapes de l'entraînement de MiniBatchKMeans les scores se stabilisent autour de -4 000.
La figure 6 présente l'évolution du score d'exactitude obtenu par le réseau de neurones sur les données de validation (des données qui n'ont été utilisées ni pour l'apprentissage de l'algorithme de clustering ni pour celui du réseau de neurones) et les données d'apprentissage. Le score d'exactitude mesure l'adéquation entre la classe prédite par le réseau de neurones et la classe de la vérité terrain. Ce score tend vers 1 lorsque les résultats du réseau rejoignent la vérité terrain.
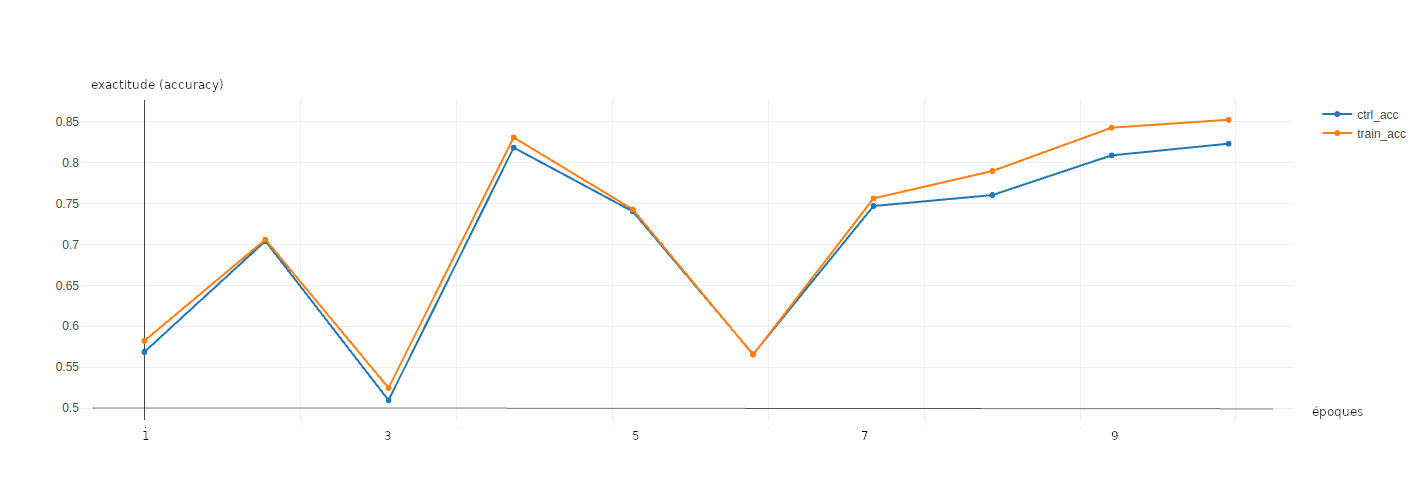
Figure 6 : évolution de l'exactitude (accuracy) sur les données de validation.
Ce score est optimale lors des dernières itérations avec une valeur supérieure à 0,8.
Enfin les figures 7 et 8 montrent l'évolution du nombre de données par groupe, au cours des itérations. Il est notable de constater que les déséquilibres entre les groupes tendent à se réduire entre les itérations 6 et 8, pour les données d’entraînement comme pour les données de validation. Lors des dernières itérations les déséquilibres entre les labels réapparaissent.
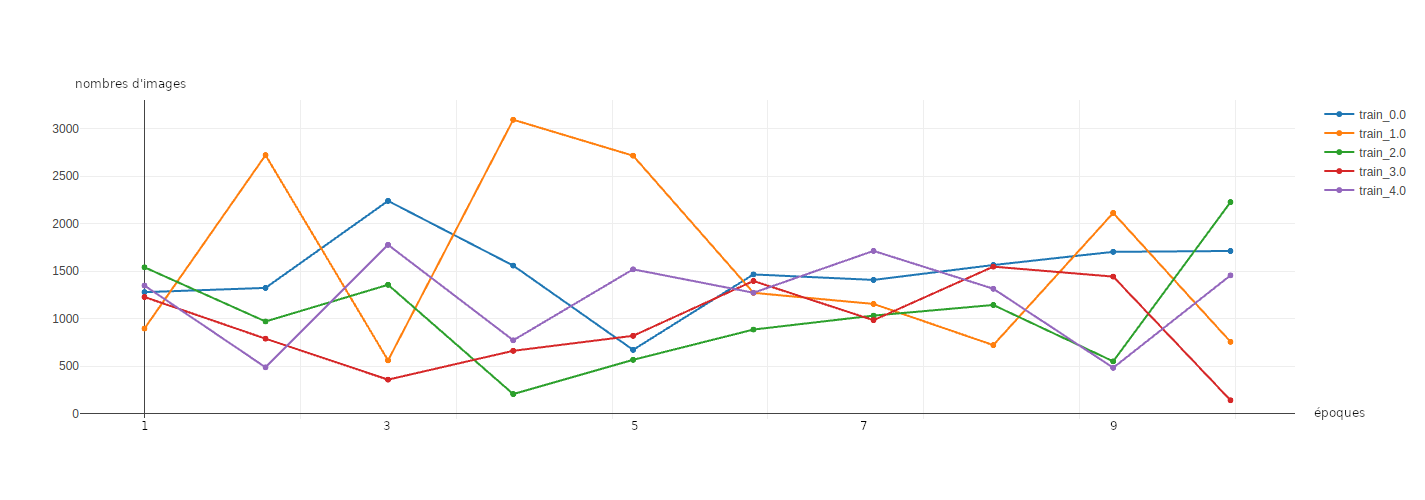
Figure 7 : évolution du nombre d'images d’entraînement pour chacun des groupes.
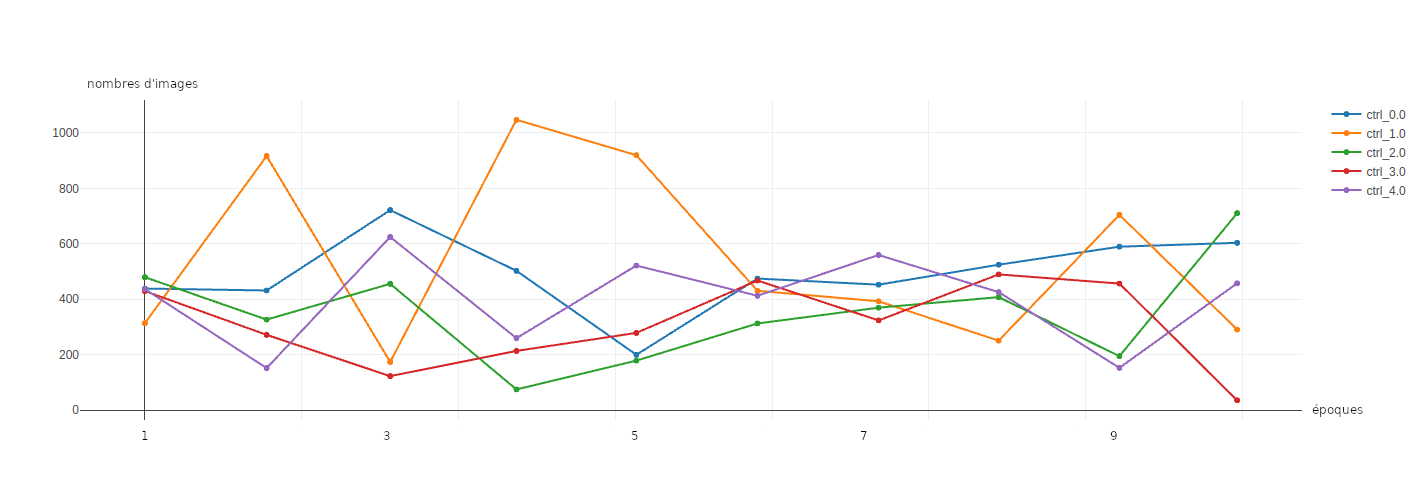
Figure 8 : évolution du nombre d'images de validation pour chacun des groupes.
Résultats et perspectives
Les figures 9, 10 et 11 correspondent à des images issues de trois clusters obtenus avec l'algorithme MiniBatchKMeans et le réseau de neurones XCeption à l'issu des 10 itérations de la méthode Deep Cluster. Durant la phase d'entraînement, Deep Cluster était paramétré pour produire 5 groupes. Nous nous assurions ainsi que lors de la phase de deep-learning, le réseau de neurones disposait d'un nombre suffisant d'images pour chaque groupe. Une fois l'entraînement terminé, afin de produire des résultats exploitables, il est souhaitable d'augmenter le nombre de groupes et de produire une sur-segmentation des images. Parmis les groupes obtenus, plusieurs pourront être fusionnés. Nous avons donc choisi d'organiser les images en 20 groupes.
Les figures 9, 10 et 11 correspondent à des images issues de trois de ces groupes. Les pondérations du réseau de neurones sont celles obtenues à la 10 eme itération. Les images sont décrites avec ce réseau, puis groupées en 20 ensemble avec MiniBatchKMeans.
Figure 9 : photographies aériennes rattachées au même ensemble.
Figure 10 : photographies aériennes rattachées au même ensemble.
Figure 11 : photographies aériennes rattachées au même ensemble.
Les groupes obtenus sont visuellement homogènes et correspondent à des paysages distincts. Utilisée directement, la méthode DeepCluster constitue donc un moyen efficace d'organiser automatiquement les quelques milliers d'images récoltées, ce qui facilite leur analyse. Lors de futur travaux nous aimerions nous concentrer sur les caractéristiques que le réseau de neurones retient pour chacun des groupes. Nous pourrions ainsi obtenir des couleurs, formes ou textures typiques de certains types de paysage.
Conclusion
L'implémentation réalisée par nos équipes de l'algorithme DeepCluster obtient des résultats similaires à ceux de Mathilde Caron et al. pour des données pourtant assez éloignées de celles d'Imagenet. Elle nous fournit, entre autre, un outil pertinent pour nos projets en lien avec les observatoires du paysages. Pour le moment le prototype développé se contente d'organiser les photographies. Nous souhaitons le faire évoluer pour qu'il nous aide à mieux caractériser les paysages en extrayant les propriétés visuelles qui leurs sont spécifiques.
Si vous souhaitez en apprendre davantage sur l'apprentissage non-supervisé et le deep-learning, jetez un oeil à nos formations.
Nous serons également ravie de tester notre version de Deep Cluster sur vos images, donc n'hésitez pas à nous contacter.
Bérengère Mathieu
Experte data science
Formations associées
Formations IA / Data Science
Formation Mise en place de projets Deep Learning avec Keras
Toulouse Du 19 au 21 mars 2025
Voir la formationActualités en lien
Image
Extraction d'objets pour la cartographie par deep-learning : évaluation du modèle
Voici le dernier article de notre série sur la cartographie par deep-learning. Après avoir expliqué comment choisir et utiliser un modèle d'extraction d'objets, nous allons maintenant en évaluer les performances. Que pouvons-nous attendre du modèle entraîné ? Quels sont ses limites et ses sensibilités ?
Image
Extraction d'objets pour la cartographie par deep-learning : choix du modèle
Deuxième article de la série sur la cartographie par deep-learning à partir d'images aériennes ou satellitaires.
Image
Extraction d'objets pour la cartographie par deep-learning : création d'une vérité terrain
Cette série d'articles parle de cartographie par deep-learning à partir d'images aériennes ou satellitaires. Dans ce 1er article, l'étape préliminaire à toute utilisation d'un modèle d'apprentissage supervisé est abordée: la création du jeu de données d'apprentissage. Notre outil geolabel-maker est mis à votre disposition pour vous aider.