Makina Blog
Cartographie 3D : Position initiale d'une caméra en fonction de la topographie d'un terrain.
Cet article explique comment on a initialisé la position de la caméra dans Geotrek 3D, en tenant compte de la topographie du Modèle Numérique de Terrain.
La position initiale de la caméra était jusque là statique, j'entends par là qu'elle était la même pour chaque profil topographique de terrain. Le problème avec cette configuration c'est que certains terrains possédent alors une orientation initiale qui leur est très défavorable :
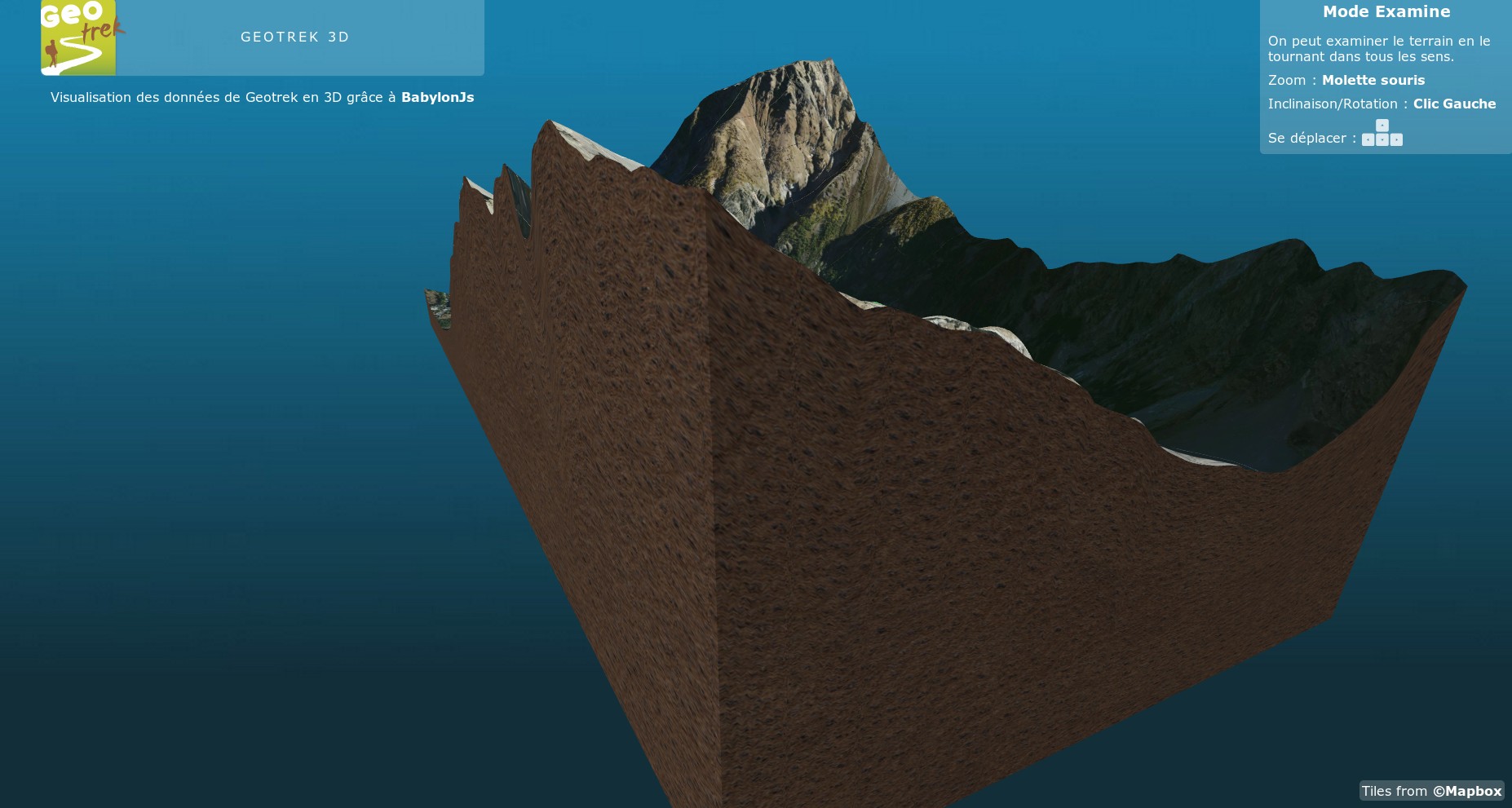
On ne voit rien et ce n'est pas très agréable de se faire tourner le dos dès le départ. Surtout que comme pour beaucoup de choses la première impression est très importante !
Il a donc bien fallu que la position initiale devienne dynamique. La question qui se pose alors, c'est comment déterminer la meilleure position initiale possible ? ou au moins comment éviter des choses comme ce qu'on vient de voir ?
Cet article montre une solution qui a plutôt bien marché dans notre cas.
J'ai appelé cette méthode la méthode des cases à indices.
L'idée principale ici est de séparer le terrain en un petit nombre de cases, et d'analyser les zones (ici appelées voisinages) qui possèdent les altitudes les plus basses. La caméra s'orientera ainsi directement sur ces zones et on ne se retrouvera pas devant un pic qui nous cache la vue.
Les cases
Tout d'abord on crée une grille de cases fictives au dessus du terrain comme ceci :

A noter que j'ai choisi un nombre de 25 cases pour avoir des résultats assez précis, tout en conservant des zones de voisinage étendues (la notion de voisinage sera explicitée plus bas).
Les types de cases
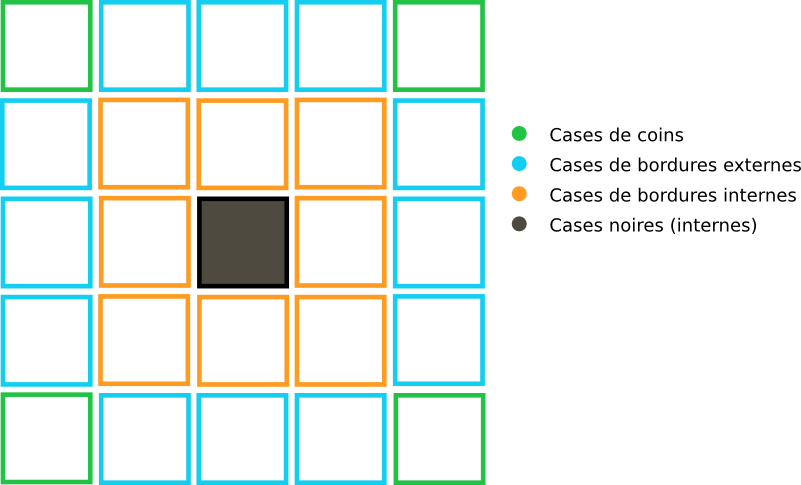
Pour faciliter la différenciation entre les cases, chacune d'elles possède un type :
Les cases de coins sont les quatre cases qui forment les angles du terrain.
Les cases de bordures externes sont les cases du bord extérieur.
Les cases de bordures internes sont les cases du bord intérieur.
Enfin, les cases internes sont les cases noires, elles n'ont ici aucune utilité.
Pour mieux comprendre, voici une visualisation en 3D de ces fameuses cases. Chaque case est représentée ici par une sphère.
 Le voisinage des cases
Le voisinage des cases
La meilleure position sera déterminée en fonction du voisinage des cases du tour. En effet, seules les cases du tour sont prises en compte car c'est elles qui potentiellement nous gâchent la vue. D'après le schéma plus haut, les cases du tour sont :
- les cases de coins qui ont un voisinage de ce type :

- les cases de bordure externe qui ont un voisinage de ce type là :

Les indices
Une fois ces cases créées on a besoin des altitudes. Pour simplifier les choses, j'ai groupé les altitudes par case et créé des indices de 0 à 10 (Avec 0 : altitudes très basses et 10 : altitudes très élevées).
C'est quand même plus facile de travailler avec des indices de 0 à 10 que de 1425,56 à 2232,124 !
Voici donc un exemple de ce que l'on peut obtenir :

Il nous faut maintenant trouver au milieu de tous ces chiffres la case alpha.
La case alpha
C'est la case qui déterminera la fameuse position initiale de la caméra. Elle possède les voisins qui ont les plus petits indices.
On parcourt donc chaque case du tour en additionnant les indices de tout son voisinage (la case courante est comprise dans le voisinage)
La case qui a le résultat le plus bas est la case alpha.
Exemple : On peut voir ici que le voisinage de la case que l'on teste a une valeur égale à 2+1+2+1+8+3 = 17, c'est le minimum de tous les voisinages.
La case testée a le voisinage le plus bas, c'est la case alpha. 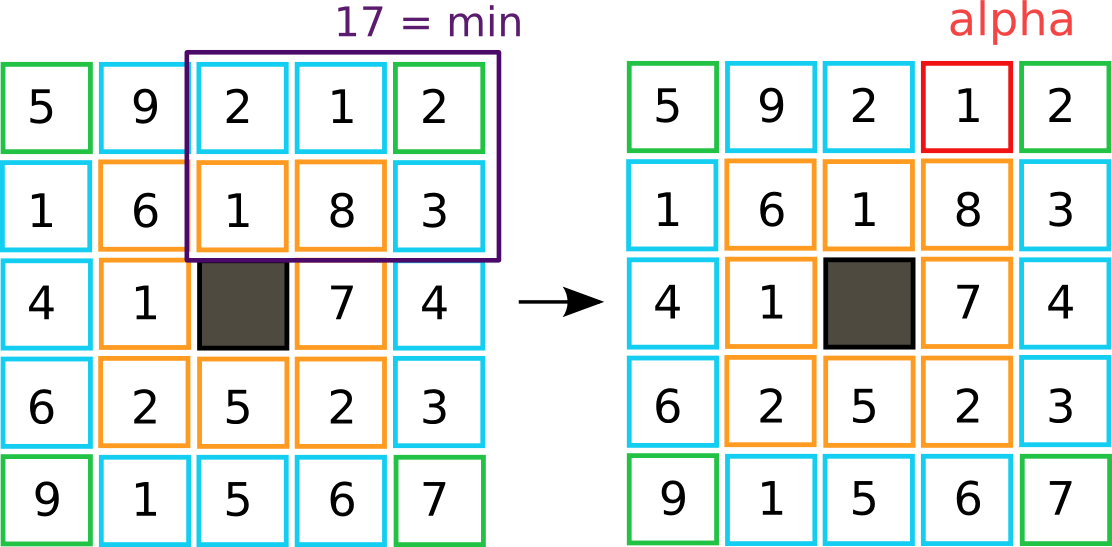
Placement de la caméra
Maintenant que l'on a trouvé la case alpha, il ne reste plus qu'à positionner la caméra en fonction de cette case.
On connait la position O du centre, on connait la position A de la case alpha, et on cherche la position C de la caméra. Un peu de mathématiques et le tour est joué !
On choisit par exemple OC = OA*3/2, ou un autre rapport, tout dépend de la promiscuité désirée entre la caméra et le terrain.
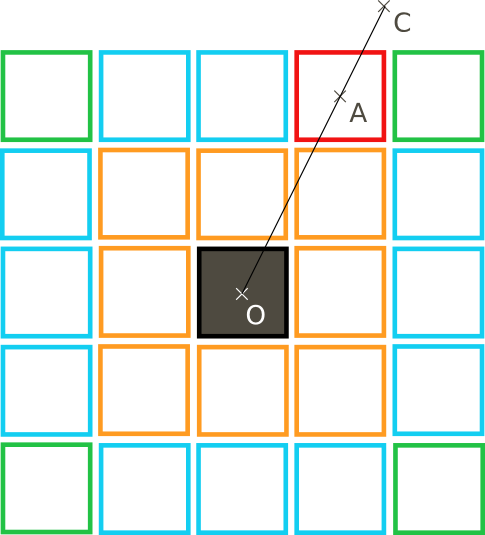
Il est vrai que plus le terrain est grand, plus la caméra sera loin de celui-ci. Mais plus il est grand, plus la caméra doit s'en éloigner pour le voir en entier !
Voici le résultat avec le même terrain qu'au tout début de l'article : 
C'est quand même beaucoup plus appréciable ! Le terrain n'est pas caché et sauf si la randonnées est dans un trou au milieu d'une montagne, on aura toujours la meilleure vue initiale ou en tout cas quelque chose qui s'en rapproche.
Formations associées
Formations SIG / Cartographie
Formation QGIS
Aucune session de formation n'est prévue pour le moment.
Pour plus d'informations, n'hésitez pas à nous contacter.
Voir la Formation QGISFormations SIG / Cartographie
Formation Leaflet
Nantes - Toulouse - Paris ou distanciel A la demande
Voir la Formation LeafletFormations SIG / Cartographie
Formation PostGIS
Aucune session de formation n'est prévue pour le moment.
Pour plus d'informations, n'hésitez pas à nous contacter.
Voir la Formation PostGISActualités en lien
Module Itinéraires ou Outdoor, lequel choisir ?
Logiciel libre
06/02/2026
Geotrek et OpenStreetMap : Mise en place d’une passerelle pour une connaissance du territoire enrichie
Logiciel libre
08/09/2025

Installer Geotrek : avec ou sans segmentation dynamique ?
Logiciel libre
08/09/2025