Depuis quelques années des initiatives internationales se mettent en place pour collecter et partager des données relatives à la biodiversité. Des projets comme celui du GBIF ou d'IDigBio permettent désormais de consulter et de récupérer des ensembles de données correspondant à des observations pour un territoire, une période ou une espèce spécifique.

La conception d'interfaces facilitant la recherche de données scientifiques ainsi que leur analyse est un domaine dans lequel de nombreuses avancées peuvent encore être effectuées. Aujourd'hui, nous allons nous pencher sur l'utilisation d'algorithmes de clustering pour proposer un regroupement pertinent des données avant de les afficher sur une carte.

Le clustering dans les grandes lignes

Le clustering est une technique d'apprentissage non-supervisé. Il consiste à grouper des données en ensembles cohérents.

L'algorithme des k-means est sans doute la méthode de clustering la plus connue. Le principe de cette technique de clustering est simple : supposons que je représente mes données comme des points dans un espace à N dimensions :

1. Je place aléatoirement K points qui seront les centres initiaux de mes ensembles ;
2. Je parcours l'ensemble de mes données et je rattache chaque donnée au centre dont elle est la plus proche ;
3. Je mets à jour chacun de mes centres en calculant la moyenne de toutes les données rattachées à un même ensemble ;
4. Je recommence à l'étape 2 jusqu'à convergence des ensembles.

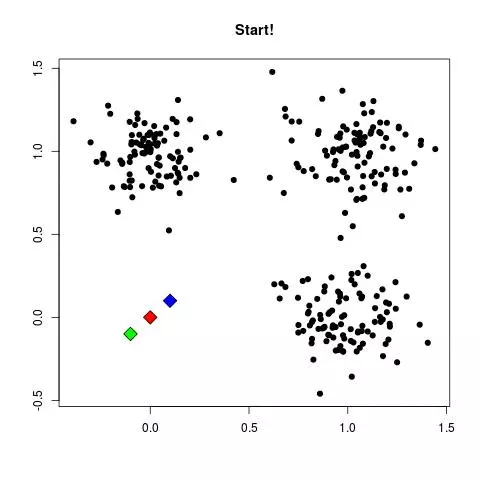
Illustration du principe, avec une animation réalisée par Mubaris NK

Le seul pré-requis nécessaire est de déterminer le nombre d'ensembles K. Pour cela, il existe deux écoles : heuristique et algorithmique. Cette distinction se retrouve dans de nombreux problèmes où une valeur optimale doit être trouvée parmi un ensemble important de valeurs.

Prenons notre problème qui consiste à trouver le bon nombre d'ensembles. Nous avons donc autant de valeurs à tester que de données, puisque les deux cas extrêmes sont :

• toutes les données dans un seul ensemble,
• un ensemble pour chaque donnée.

Une méthode est dite heuristique si elle propose rapidement une solution en explorant qu'un nombre restreint de valeurs possibles. En contrepartie il n'existe aucune garantie que la réponse fournie soit la meilleure. Un peu comme si vous comptiez le nombre de chaussettes chez vous : vous allez vous concentrer sur la chambre qui est la pièce où le plus grand nombre de chaussettes seront présentes, mais vous omettrez les chausettes qui traînent malencontreusement dans la salle de bain et la cuisine. La méthode du coude est une méthode heuristique fréquemment utilisée pour sélectionner le nombre d'ensembles à étudier.

A contrario d'autres algorithmes recherchent une solution optimale en testant l'ensemble des valeurs possibles. Ainsi en 2001, les chercheurs R. Tibshirani, G. Walther et T. Hastie ont proposé l'algorithme de « Gap Statistic » capable d'analyser automatiquement les données et d'en extraire le meilleur nombre de clusters.

Tous les chemins mènent à Rome

… Mais certains sont plus courts que d'autres

Dans le cadre de notre application les données sont les coordonnées GPS (latitude et longitude) du lieu où un spécimen d'une espèce a été observé. La latitude et la longitude étant des données angulaires, la distance euclidienne utilisée par l'algorithme k-means pour trouver le centre le plus proche peut ne pas fournir une valeur cohérente avec la réalité.

Pour bien comprendre, regardons le calcul qui est effectué pour la distance euclidienne :

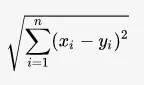
et prenons un cas concret avec :

• Suva, la capitale de Fidji, latitude -17.55163, longitude -149.55848 ;
• Papeete, une commune de Polynésie Française, latitude -18.12481, longitude 178.45008.

À vol d'oiseau ces deux endroits ne sont pas très loin :

Mais comme nous passons d'une longitude négative à une longitude positive, la distance euclidienne nous donne une valeur supérieure à 328. De manière plus concrète, c'est comme si notre oiseau ne partait pas dans la bonne direction :

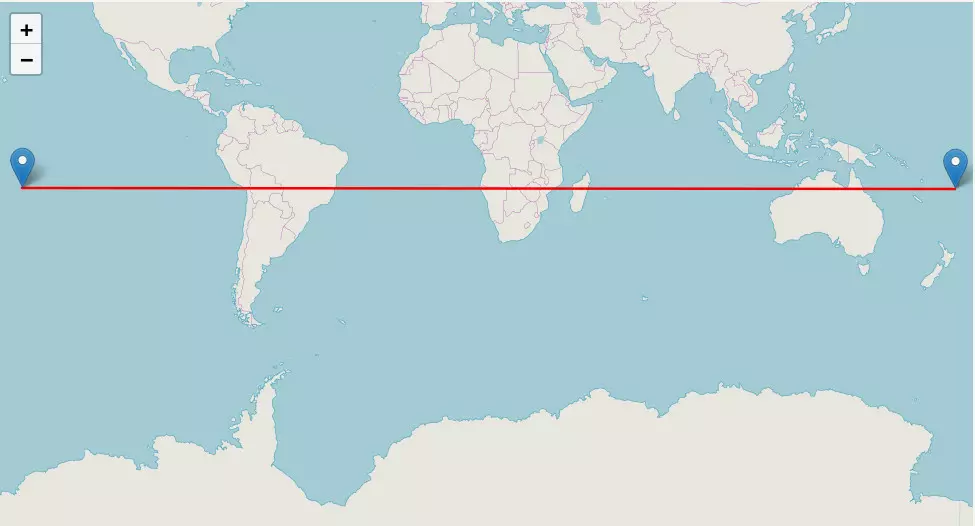
Heureusement il existe d'autres méthodes de calculs de distances possibles, capable de manipuler des données angulaires. Cependant ces dernières ne sont pas utilisables avec k-means.

Nous nous sommes donc tournés vers un algorithme plus générique : HBDSCAN.

Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN)

Par rapport à k-means, HBDSCAN apporte trois améliorations :

• il gère n'importe quel type de distance ;
• il fait du clustering hiérarchique ;
• il est capable de détecter du bruit : c'est-à-dire des données n'appartenant pas à l'ensemble le plus proche.

Ce dernier point est essentiel : dans le cadre de notre application, il se peut très bien que certaines observations apparaissent de manière sporadique, dans des lieux éloignés des centres. Nous ne voulons pas modifier la structure de nos groupes en les forçant vaille que vaille à rejoindre un ensemble.

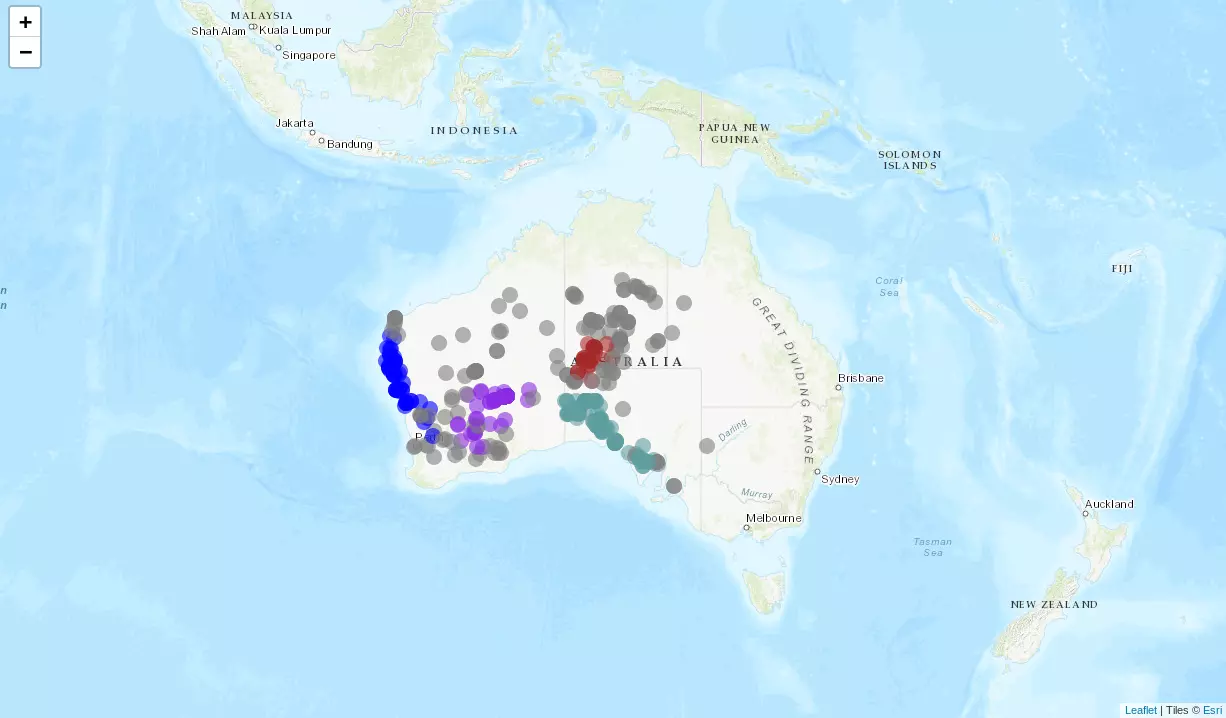
Pour comprendre le principe de HDBSCAN, prenons un cas concret, le Moloch horridus ou Diable Cornu :

L'Atlas of Living Australia nous permet de récupérer presque 2000 observations de la bêbête et d'en observer la répartition sur une carte :

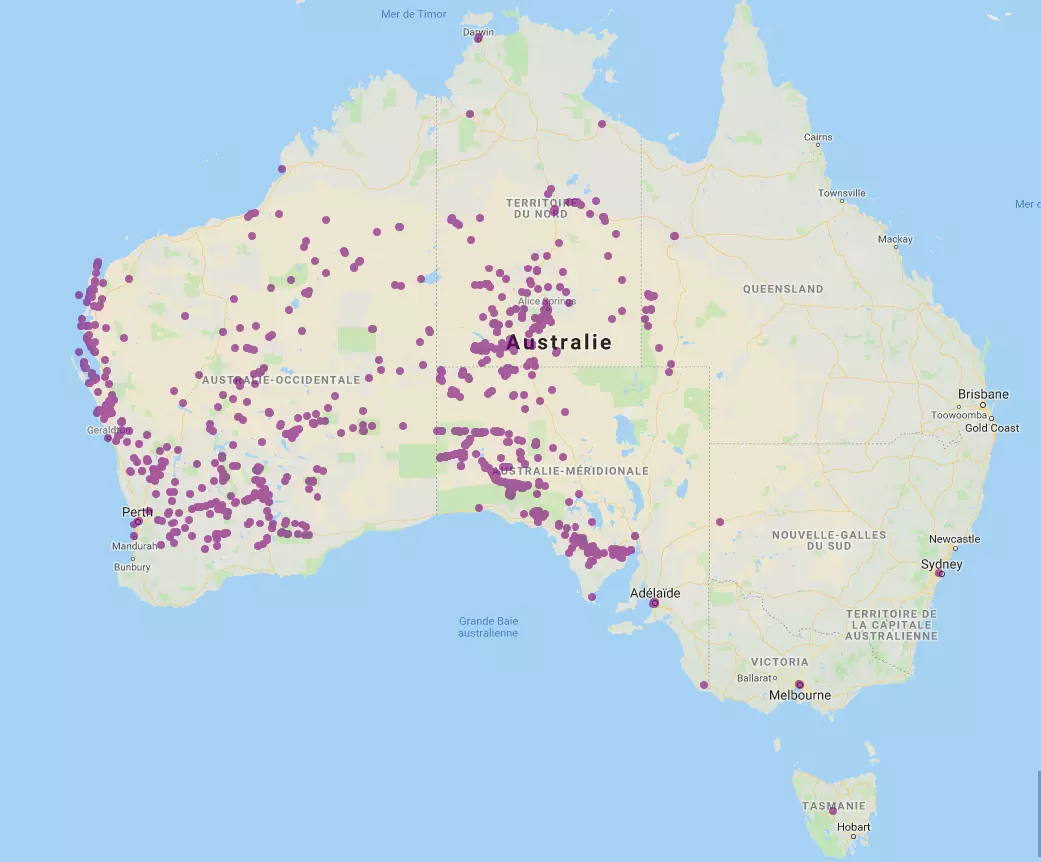
Ces observations peuvent par exemple être réparties en trois ensembles avec :

• un groupe en Australie occidentale
• un autre en Australie méridionale
• et un dernier sur le territoire nord

Des données vers la mesure de densité

La première étape pour HBDSCAN consiste à déterminer à partir des données observées à une mesure de la densité. Sur l'exemple précédent, certaines zones comptent de nombreuses observations de notre diable cornu (la cote de l'Australie méridionale). Pour d'autres, comme la Tasmanie, ces observations sont beaucoup plus éparses.

Mais comment quantifier cette densité ? Pour chaque point nous regardons sa distance maximum avec ses k plus proches voisins. Si cette distance est importante, alors le point appartient à une zone de moindre densité, à l'instar des observations du diable cornu en Tasmanie. Nous notons cette distance aux k plus proches voisins k_nearest.

L'étape suivante consiste à accentuer les écarts entre les points. Soient a et b, deux observations de notre petit diable. La distance entre a et b devient :

d_new(a,b) = max(k_nearest(a), k_nearest(b), d(a,b)) 

où d est simplement la distance choisie pour estimer si deux points sont proches (il peut s'agir de la distance euclidienne).

Plus vous prenez en compte de voisins, plus vous aurez tendance à augmenter les écarts entre les points. L'une des conséquences immédiates est que davantage de données seront écartées des ensembles construits.

Dessine moi un arbre couvrant

Troisième étape : construire un arbre couvrant à partir des données. Pour cela supposons que chacune des observations correspond au sommet d'un graphe. Ces sommets sont reliés entre eux par des arêtes pondérées, où la pondération est la distance d_new entre ces deux données.

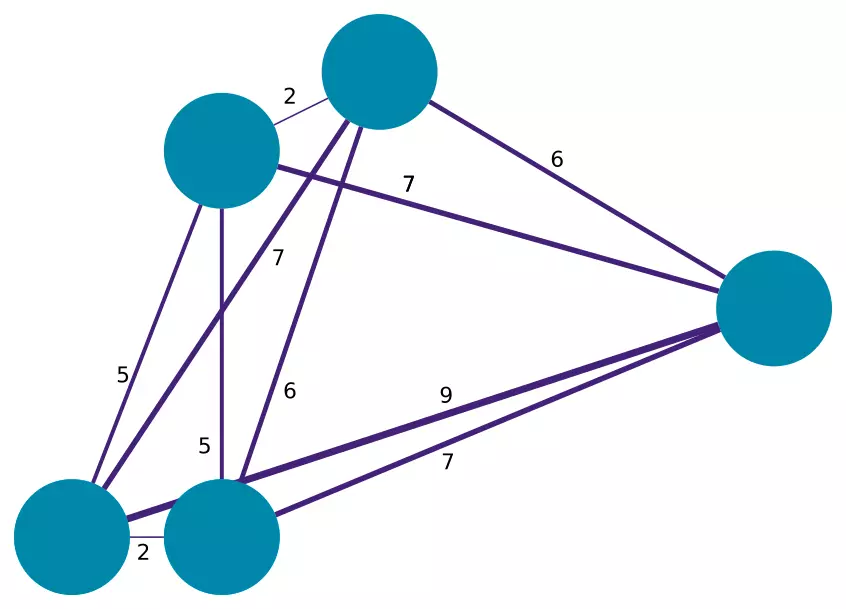
Un exemple de graphe pondéré : plus les arêtes sont fines, plus les sommets sont distants.

À partir de ce graphe HBDSCAN recherche un arbre couvrant (ou plus précisément un sous ensemble des arêtes) de manière à ce que tous les sommets soient connectés et qu'il n'y ait pas de cycle (de boucle) entre plusieurs sommets. En voici un exemple :

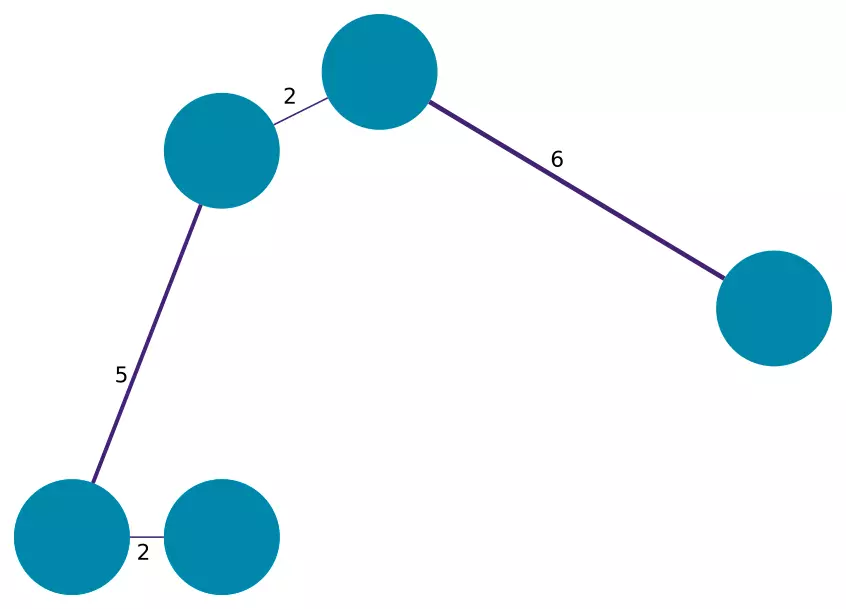
Malgré cette première règle, il existe encore de nombreuses possibilités d'arbres couvrants. HBDSCAN va en construire un de manière à ce que la somme des pondérations des arêtes soit minimale.

Clustering hierarchique

Une fois l'arbre couvrant trouvé, HBDSCAN va regrouper les données en ensembles hiérarchisés. Il commence par trier les arêtes dans l'ordre décroissant. Il sélectionne la première arête, celle pour laquelle la distance est maximale et fusionne les deux sommets dans un même ensemble.

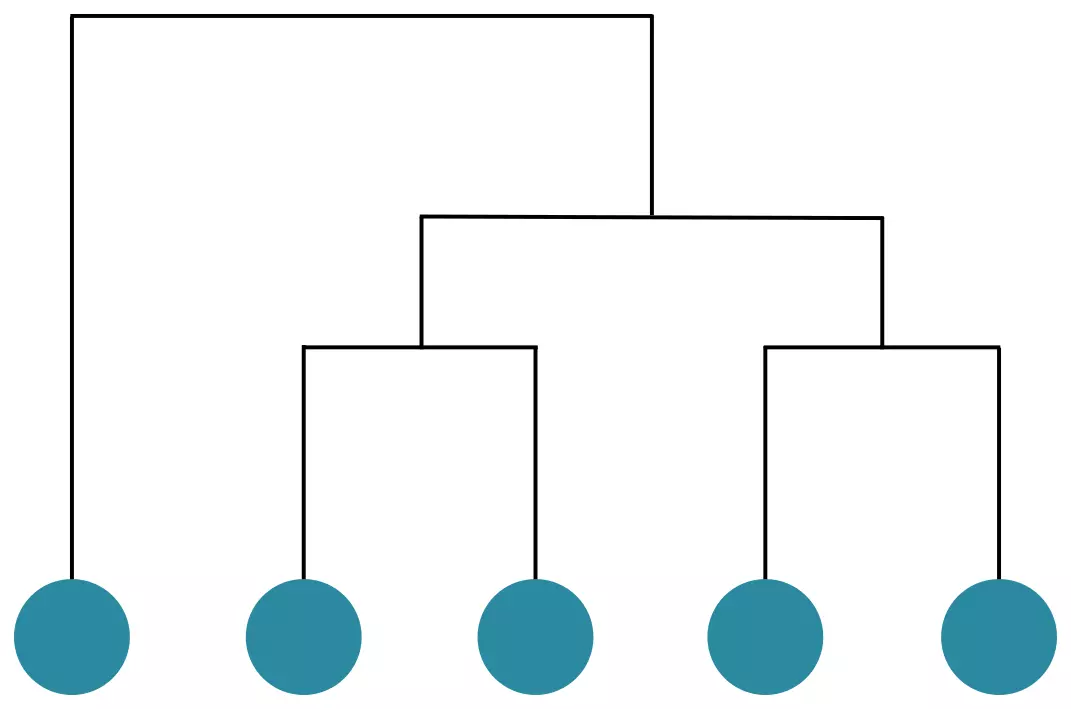
Le résultat correspondant à l'arbre couvrant précédent.

Condenser les ensembles

Sur notre exemple précédent la hiérarchie n'est pas très complexe. Mais avec plusieurs centaines voire plusieurs milliers de données, il devient nécessaire d'élaguer le résultat.

Pour créer un dendrogramme dit condensé, HDBSCAN utilise un paramètre : la taille minimum des ensembles (_m_). Il parcourt la hiérarchie et pour chaque lien horizontal reliant plusieurs données dans un même ensemble, il s'interroge sur les conséquences de la suppression de chaque lien en comparant chaque descendant e1 et e2 avec le paramètre _m_ :

• si les deux ensembles ont une taille supérieure à m, alors la séparation de l'ensemble parent en deux ensembles e1 et e2 est validée et conservée dans la hiérarchie ;
• si l'un des deux ensembles créés, e1 par exemple, contient un nombre de données inférieures à _m_ :
  • l'ensemble le plus grand, e2, est considéré comme une version modifiée de l'ensemble parent ;
  • l'ensemble le plus petit, e1, est considéré comme artéfact ;
  • seul le lien entre e2 et l'ensemble parent est conservé ;
  • la perte des données de e1 est quantifiée selon la distance e1 - e2 : plus cette distance est grande, plus il est probable que ces données soient un artéfact.

Extraire les ensembles

Une fois le clustering hiérarchique des ensembles établi, il convient de distinguer les ensembles les plus pertinents. HDBSCAN se base sur le temps d'existance d'un ensemble comme critère de sélection. Un ensemble est conservé s'il persiste dans le temps, c'est-à-dire s'il ne se divise pas rapidement en sous-ensembles. Dans le cas contraire, il est relégué. Une règle implicite en découle : si un ensemble est selectionné alors aucun de ses enfants (si division il y a lieu) ne peut être considéré comme étant lui-même un ensemble persistant.

Pour déterminer cette durée de vie, il est nécessaire de définir pour un ensemble donné le moment de naissance λ(birth) jusqu'à sa prochaine division λ(death). Avec ces données, il est désormais possible de calculer la stabilité d'un ensemble selon la formule :

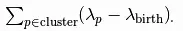
Ainsi pour chaque lien horizontal hiérachique, la somme de la stabilité du groupe et de ses descendants est calculée et si la stabilité d'un ensemble est supérieure à la somme de ses descendants alors c'est un ensemble.

Revenons à nos diables

Avec un échantillon de N = 400 observations de Moloch horridus, nous avons choisi une valeur minimale de taille de clusters m = 22.

À partir de ces données, chacune des cinq étapes décrites précédement a été réalisée.

 

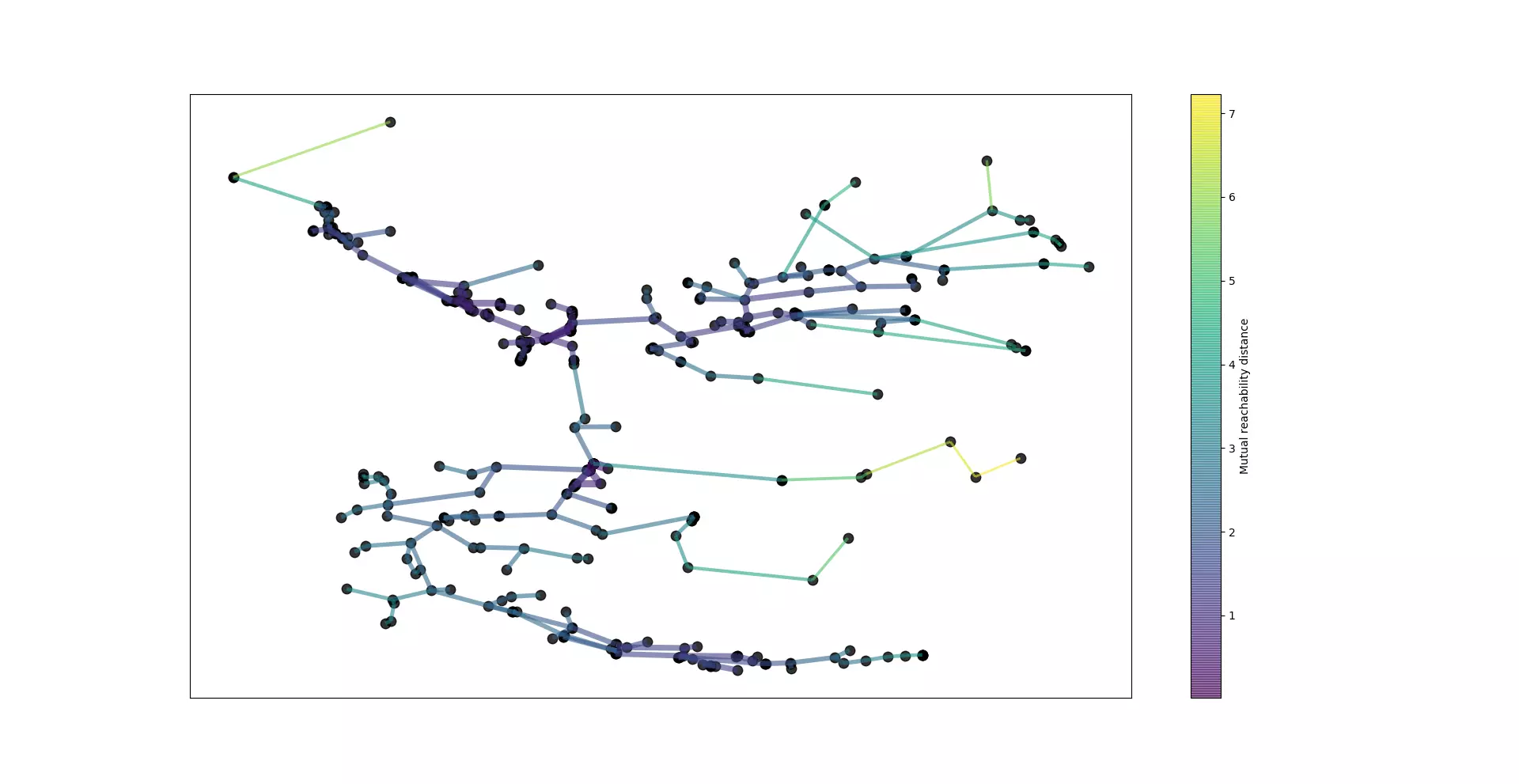
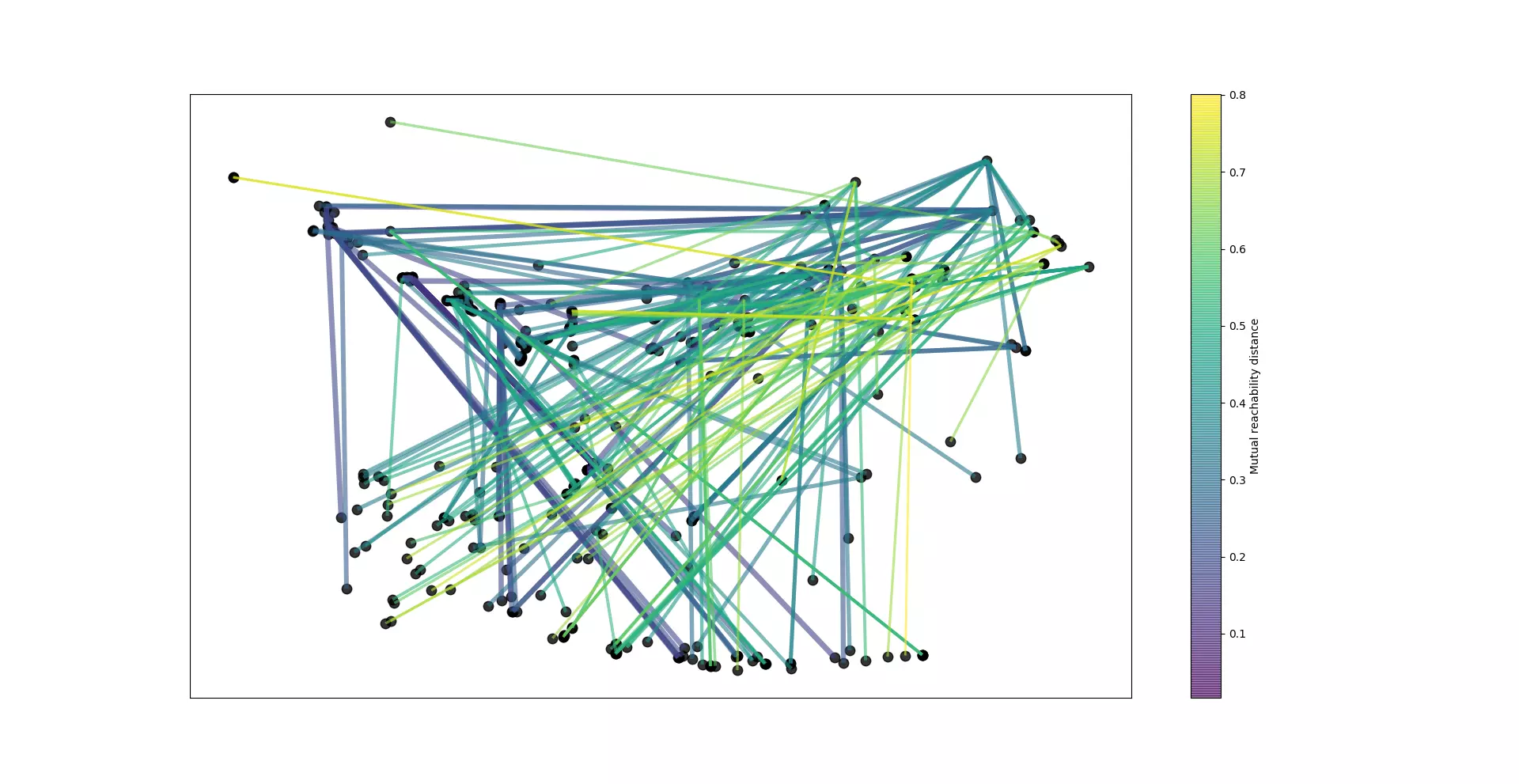
Dans le cas de la première figure, la distance euclidienne a été utilisée pour calculer la densité. La seconde figure utilise quant à elle la formule de Haversine pour calculer la distance entre deux points (et donc la densité pour chaque point). La différence entre ces deux figures illustrent l'impact du choix de la distance dans la construction des ensembles.

N.B. Les résultats suivant du clustering ont été calculés uniquement avec la distance haversine.

 

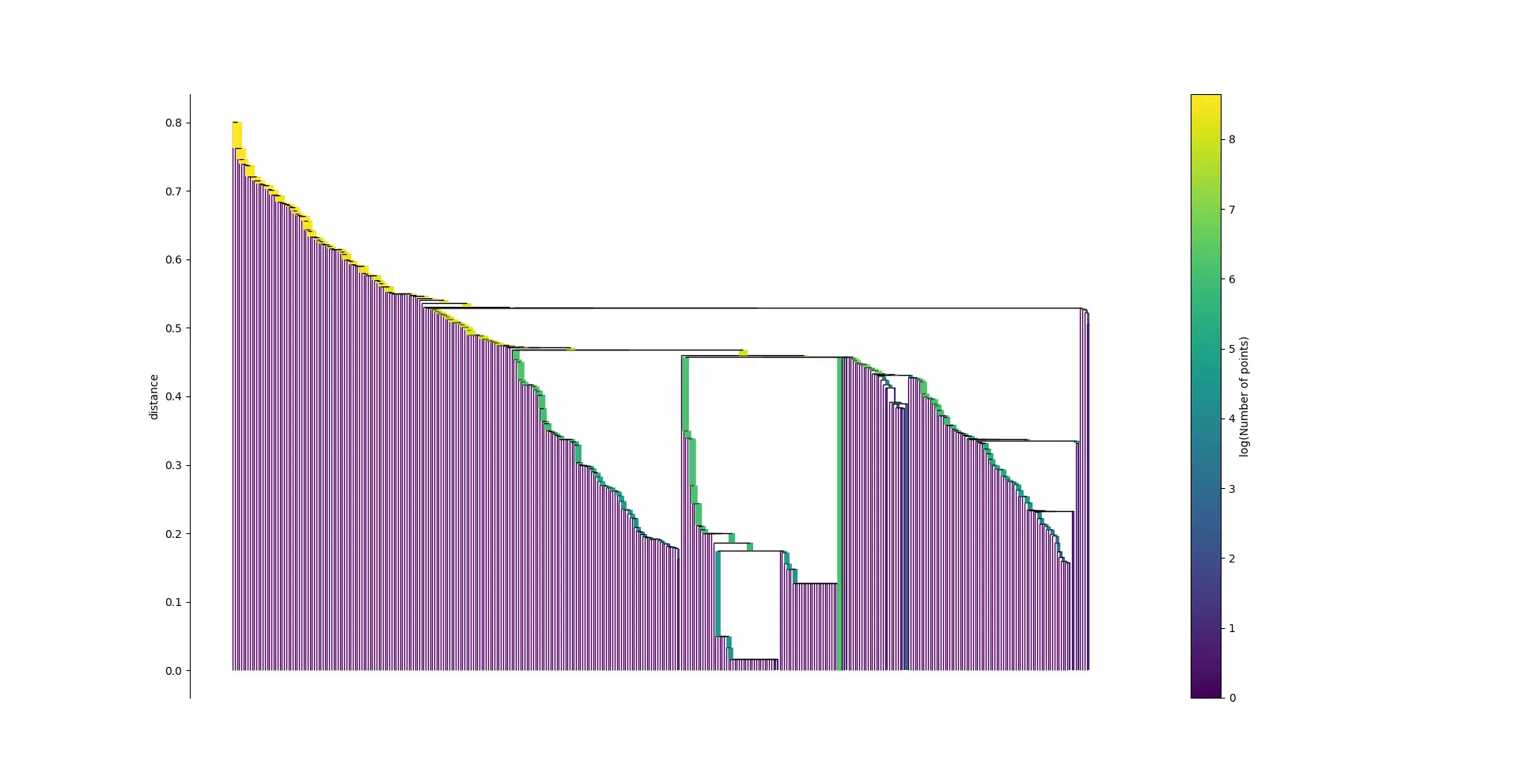
Une fois ces deux graphiques réalisés, la sélection des ensembles est effectuée. Au final, quatre clusters ont été trouvés. Il reste donc maintenant à afficher ces ensembles sur la carte.

Choix du paramètre m

Nous avons effectivement passé sous silence la sélection de ce paramètre dans la partie précédente pour une bonne raison.

Contrairement à k-means, il n'existe pas à ce jour de méthodes heuristiques ou algorithmiques pour déterminer une valeur approchée ou optimale.

Néanmoins, il existe un phénomène de convergence suivi d'une perte d'informations. En effet en augmentant progressivement le paramètre _m_, on remarque une stagnation du nombre d'ensembles trouvés. De même, une diminution de la taille des ensembles est visible. De plus en plus de points sont considérés comme du bruit.

Pour autant, l'atteinte de ce palier ne garantit pas que le nombre d'ensembles trouvés soit optimal.

Par conséquent, des outils supplémenataires ont été mis en place afin de laisser à l'utilisateur le choix de déterminer la valeur optimale de _m_ selon les données étudiées.

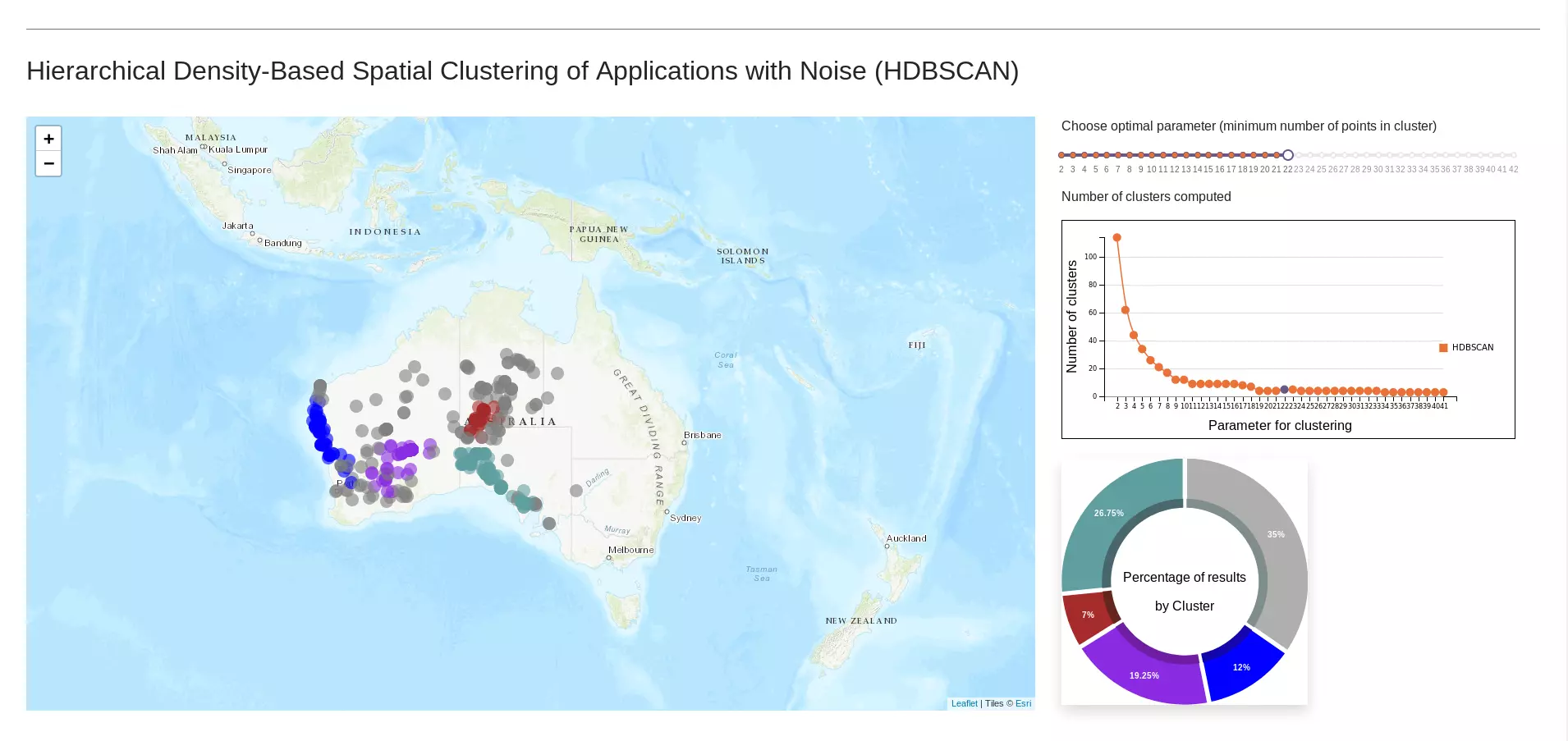
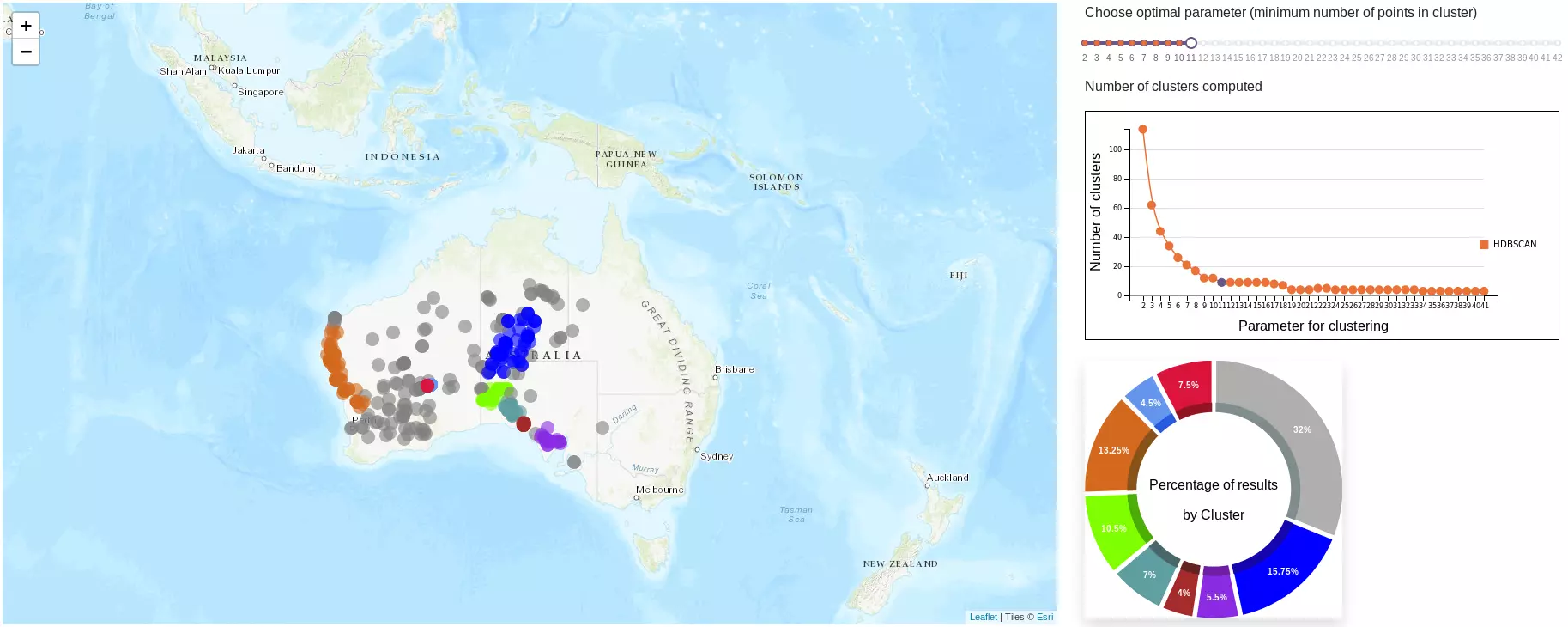
Exploration des clusterings possibles

L'objectif est de donner la liberté à l'utilisateur de visualiser les différentes possibilités de clustering. Pour cela, une réglette a été mise en place. Elle est accompagnée d'un graphique représentant le nombre d'ensembles trouvés en fonction du paramètre _m_. Ce dernier a deux fonctions :

• limiter les appels à la méthode HDBSCAN (via l'API) puisque l'utilisateur connaît déjà le nombre d'ensembles trouvés et donc il ne va pas déplacer la réglette à chaque position possible;

• visualiser l'effet de stagnation/convergence du nombre d'ensembles.

  L'association de ces deux éléments permet d'améliorer le ressenti de l'utilisateur en l'accompagnant dans la recherche d'ensembles pertinents.

Analyse de la répartition des données entre les ensembles

Si on ce concentre sur la visualisation des données, la lecture de la carte est insuffisante pour appréhender la taille des ensembles. La superposition des points à de telles coordonnées géographiques empêche la mise en exergue de la proportion de points appartenant à un ensemble. Pour pallier ce problème, un diagramme représentant le pourcentage d'observations est affiché.