History of new and old algorithms usages

The history of the algorithm change is described in the article « Python 2.3 Method Resolution Order ». This blog tries to summarize it and explaining the main part using Python simple examples.

When new and old algorithms are used ?

If MRO has changed with Python 2.3 you may think that the new algorithm is used with all Python versions after 2.2.
Not exactly. To keep compatibility between Python versions, the new MRO algorithm is only used with what is so called « new classes ».
New classes are classes whose first parent ineherits from Python root « object » class.

So in Python 2, if you create this class hierarchy :

class A :
    pass
class B :
    pass
class C(A, B) :
    pass

C instances will use the old Method Resolution Order algorithm because none of the classes are derived from the Python « object » root class.

If you change above code with:

class A(object) :
    pass
class B(object) :
    pass

Then, the MRO will be based on the new algorithm.

About Python 3 :

In Python 3 each class inherits from the root « object » class. Even if you do not indicate this explicitly. So the new algorithm will be used in both cases above with Python 3.
Be careful : This can cause unexpected changes in your software when migrating from Python 2 to Python 3.

Understanding old classes MRO

Python is an interpreted language, so it is easy to try/test any kind of things.
Lets discover by ourselve how works the old classes method search path.

Run this script using Python 2:

class A:
    def who_am_i(self):
        print("I am a A")

class B(A):
    def who_am_i(self):
        print("I am a B")

class C(A):
    def who_am_i(self):
        print("I am a C")

class D(B,C):
    def who_am_i(self):
        print("I am a D")

d1 = D()
d1.who_am_i()

$ python2 Python-MRO.py  
I am a D

Now comment the who_am_i method in D:

class D(B,C):
#    def who_am_i(self):
#        print("I am a D")
    pass

Which one will be called ?
The one from B, from C or from A ? Well, everybody should be ok to say « the one from B or C » as every class method is virtual in Python.
And the answer is :

$ python2 Python-MRO.py  
I am a B

Ok. Nobody is surprised.
Now, lets comment the who_am_i method in class B:

class B(A)
#     def who_am_i(self):
#         print("I am a B")
    pass

And now, which method will be called when calling d1.who_am_i() ? C or A ? Well, many of you, me first, may agree it should be C as C is another direct parent of class D !

python2 Python-MRO.py  
I am a A

But method from A is called !
Well, what's this ?
Before explaining this behaviour, lets continue the exercice to its end.
Now comment, the who_am_i method in class A and run the script again.

class A:
#     def who_am_i(self):
#         print("I am a A")
    pass

python2 Python-MRO.py  
I am a C

Now, uncomment the who_am_i method in A and make A inherits from object.

class A(object):
     def who_am_i(self):
         print("I am a A")

And run again the script :

python2 Python-MRO.py  
I am a C

You could also remove the object from A parent list and run the script with Python 3 :

class A():
     def who_am_i(self):
         print("I am a A")

python3 Python-MRO.py  
I am a C

So, why Python search for A before C when A does not inherits from object in Python 2 ?
This is due to the old classes MRO algorithm behaviour. It is a very simple and easy to understand algorithm :
When a class inherits from multiple parents, Python build a list of classes to search for when it needs to resolve which method has to be called when one in invoked by an instance.
This algorithm is a tree routing, and works this way, deep first, from left to right :
1. Look if method exists in instance class
2. If not, looks if it exists in its first parent, then in the parent of the parent and so on
3. If not, it looks if current class inherits from others classes up to the current instance others parents.

So in our example, algorithm search path is : D, B, A, C, A.
A class cannot appears twice in search path, so the final version is D, B, A, C:

• Looking in D
• If not found, looking in B
• If not found, looking un B first parent A
• If not found, going back in B others parents (none)
• If not found, looking in D others parents : C

So, using this class hierarchy:

class A1():
#      def who_am_i(self):
#          print("I am a A1")
    pass

class A2():
     def who_am_i(self):
         print("I am a A2")

class A3():
     def who_am_i(self):
         print("I am a A3")

class B(A1, A2):
#     def who_am_i(self):
#         print("I am a B")
    pass

class C(A3):
    def who_am_i(self):
        print("I am a C")

class D(B,C):
#     def who_am_i(self):
#         print("I am a D")
    pass

d1 = D()
d1.who_am_i()

The search path when invoking d1.who_am_i() is : D, B, A1, A2, C, A3
So, it should display « I am A2 » as nor D, nor B, not A1 defines the who_am_i method()

python2 Python-MRO-2.py  
I am a A2

Understanding the new algortihm

As seen at the end of first exercice, when the class inherits from Python root object the behaviour changes.
If you run the first script using python3 the algorithm behaviour change too.
This is because in Python 3 or in Python 2 using object as a parent class the new MRO algorithm is used.

A near exact, but not completly exact, as we will see at the end of the article, definition of the new classes algorithm is that it is the same than the old one, except with this difference : each time a class is found in built search path, Python asked the question « Is it a good head ? » and if not, it removes the class from the final search path.
So, what is a « good head »?
A class is said as being a « good head » if there is no other class in the tail of the search path which inherits from it. In this case it is more natural to use the method defined by its derived class.

So, in script 1, the search path (tree routing without simplification) is D, B, A, C, A.
Once built, Python tries to remove duplicated entries using the "good head" question. D and B are good head as there is no derived class in the tail of the path after they position which inherits from them.

When it is the first class A occurence, Python ask to class A : « Are you a good Head » ? And the answer is « No, I've have not been very kind today, I've tried to stole the place of my child class C which inherits from me and is in the the tail of the search path after me ». So Python removes A from the search path at this point which becomes D, B, C, A.

What about the second script. Search path is D, B, A1, A2, C, A3.
A2 is apparently a good head, so it should be used when D, B and A1 « who_am_i » method are commented with Python 3 :

python3 Python-MRO-2.py  
I am a A2 

But if C inherits from A2 rather than A3, C should be returned :

class C(A2):
    def who_am_i(self):
        print("I am a C")

python3 Python-MRO-2.py  
I am a C 

Ok. Personnaly I would have prefer to use a Method Resolution Order looking from left to right then deep inside left and so on to choose the good method to call because it seems to me more natural that when D inherits from B and C that their method is called first before any of their parents : D is a B or a C before being a parent of them.

That's my point of view.

Impossible Method Resolution

With the new algorithm, sometimes no good path can be found to solve method resolution.
This example shows such conflict :

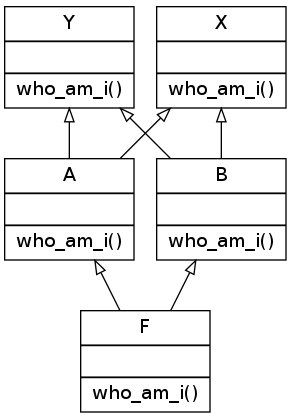
class X():
    def who_am_i(self):
        print("I am a X")
    
class Y():
    def who_am_i(self):
        print("I am a Y")
    
class A(X, Y):
    def who_am_i(self):
        print("I am a A")
    
class B(Y, X):
     def who_am_i(self):
         print("I am a B")

class F (A, B):
    def who_am_i(self):
        print("I am a F")

$ python2 Python-MRO.py  
I am a F

In Python 2, search path is F, A, X, Y, B (Note that the search path described for this example in the link to the original article given at the top of this article is wrong).

With Python 3, search path should be : F, A, X, Y, B, Y, X and after removing « bad heads » : F, A, B, Y, X regarding my explanations above.

$ python3 Python-MRO.py  
Traceback (most recent call last): 
  File "Python-MRO.py", line 76, in <module> 
    class F (D, E): 
TypeError: Cannot create a consistent method resolution 
order (MRO) for bases C, B 

So, what's happened here ?
The algorithm described before for Python 3 is not exactly the real one.
Here is the definition of linearization algorithm used to defined the search path ;
The linearization of a class C is the sum of C plus the merge of the linearizations of the parents and the list of the parents.
In symbolic notation:
L[C(B1 … BN)] = C + merge(L[B1] … L[BN], B1 … BN)
So in our case L[F(A, B)] = F + merge(L[A], L[B], A, B)

And the algorithm to merge linearized lists is:

1. Take the head of the first list, i.e L[B1][0];
2. If this head is not in the tail of any of the other lists, then add it to the linearization of C and remove it from the lists in the merge,
3. Otherwise look at the head of the next list and take it,
4. If it is a good head. Then repeat the operation until all the class are removed or it is impossible to find good heads.
5. In this case, it is impossible to construct the merge, Python 2.3 will refuse to create the class C and will raise an exception.

L[A(X, Y)] = A + merge(L[X], L[Y], X, Y) = A, X, Y
L[B(Y, X)] = B + merge(L[Y], L[X], Y, X) = B, Y, X

So, L[F(A, B)] = F + merge( (A,X, Y) + (B, Y, X), A, B)
So, applying the algorithm, A is a good head, so we keep it :
L[F(A, B)] = F, A + merge( (X, Y) + (B, Y, X), B)
So applaying the algorithm, X is not a good head as it appears in the tail of (B,Y, X), so we skip it and continue with next list to merge : (B, Y, X).
B is a good head, so we keep it :
L[F(A, B)] = F, A, B + merge( (X, Y) + (Y, X))
So, applying the algorithm X is not a good head as it appears in the tail of (Y, X) so we skip it and jump to (Y, X). Y is not a good head too as it appears in the head of (X, Y). So we continue to the next list. But there is no other. Thus, Python 3 cannot linearize the class F to build the MRO and raise the exception !

That's it. You now know how the whole mecanism works.
This is not so complicated, but not so easy to guess by yourself, even by testing the language behaviour as this last script exception cannot be guessed by yourself if you do not have the Pythonic explanation on how this is implemented.

Hope this will help you understanding the magic of Python.