Makina Blog
Localisation d'un objet par classification de superpixels
Dans ce tutoriel, vous apprendrez comment réaliser un programme Python capable d'apprendre à localiser un objet au sein d'une image.
Introduction
La vision par ordinateur est une branche de l'intelligence artificielle qui regroupe un ensemble d'algorithmes permettant à une machine d'analyser son environnement, à partir de photographies ou vidéos. Actuellement, deux concepts sont à l'origine d'avancées notables :
- les superpixels, qui sont un moyen de résumer l'information contenue dans une image
- l'apprentissage automatique supervisé, qui comprend une série de méthodes capables d'apprendre à prédire des comportements ou à classer des données, à partir de quelques exemples.
Nous allons voir comment en combinant l'un et l'autre, nous pouvons produire un programme capable d'identifier et de localiser les objets constituants une photographie. Nous utiliserons comme exemple, la photographie suivante :

Photographie du Pan d'Etosha, mise à disposition sur Wikimedia Commons.
Nous chercherons à différencier le ciel, l'herbe et l'arbre. Notre programme sera développé en Python. Nous utiliserons les bibliothèques :
- Numpy pour calculer efficacement les caractéristiques des données ;
- Scikit-image et Scipy pour les traitements sur les images
- Scikit-learn pour les méthodes d'apprentissage automatique
- Matplotlib et Seaborn pour la visualisation des résultats
Les superpixels
Les superpixels correspondent à de petits groupes homogènes de pixels voisins. Ils ressemblent à un ensemble de pièces de puzzle, qui une fois assemblées permettraient de retrouver les différents objets constituant une image. En vision par ordinateur, les superpixels sont principalement utilisés pour des raisons d'efficacité. Comme chaque superpixel regroupe quelques centaines de pixels similaires, manipuler les superpixels à la place des pixels réduit considérablement le nombre d'entités à traiter.

Notre image, sur-segmentée en 3106 superpixels
Par exemple, notre photographie contient 903 600 pixels (1200 pixels en largeur et 753 en hauteur). En regroupant ces derniers en 3106 superpixels et en attribuant à chaque pixel la couleur moyenne du superpixel auquel il appartient, nous perdons quelques détails mais l'image reste lisible.
SLIC
L'algorithme SLIC (Simple Linear Iterative Clustering) est sans doute l'une des méthodes les plus célèbres pour découper une image en superpixels. Son principe général est le suivant :
- les pixels sont groupés en superpixels rectangulaires et réguliers
- chaque superpixel est décrit par sa couleur moyenne et la localisation de son barycentre
- chaque pixel est ré-attribué au superpixel dont il est le plus proche en terme de couleur et de localisation
- les étapes 2 et 3 sont répétées jusqu'à ce que les superpixels soient stables
La rapidité de SLIC et la qualité des résultats qu'il produit lui ont garanti une immense popularité dans les méthodes de vision par ordinateur. Plusieurs implémentations de cet algorithme sont disponibles. Nous allons utiliser celle de la bibliothèque Scikit-image.
from skimage.segmentation import mark_boundaries
from skimage.segmentation import slic
import matplotlib.pyplot as plt
import scipy.misc as im
from sklearn import svm
import seaborn as sns
import numpy as np
path_img = 'mon_image.jpg'
# charger une image
img = im.imread(path_img)
# utilisation de l'algorithme SLIC
superpixel_labels = slic(img, n_segments=3000, compactness=10)
# récupérer les canaux de couleur de l'image
red = img[:, :, 0]
green = img[:, :, 1]
blue = img[:, :, 2]
# recuperer le nombre de superpixels
nb_superpixels = np.max(superpixel_labels) + 1
# attribuer la couleur moyenne de chaque superpixel
# aux pixels lui appartenant
for label in range(nb_superpixels):
idx = superpixel_labels == label
red[idx] = np.mean(red[idx])
green[idx] = np.mean(green[idx])
blue[idx] = np.mean(blue[idx])
# dessiner les bordures des superpixels en noir et blanc
img = mark_boundaries(img, superpixel_labels, \
color=(1, 1, 1), outline_color=(0, 0, 0), \
mode='outer')
# afficher le résultat
plt.imshow(img)
plt.show()
En plus de l'image, deux paramètres sont fournis à la fonction SLIC : le nombre de superpixels désirés (n_segments) et un paramètre de compacité (compactness), qui dose l'influence de la localisation du pixel par rapport à sa couleur. Nous avons indiqué souhaiter 3000 superpixels. Notons que la valeur de ce paramètre est légèrement différente du nombre réel de superpixels produits (3106). Une compacité élevée favorise des superpixels réguliers, proche des rectangles initiaux. Généralement, il est recommandé de donner une valeur entre 10 et 20. Au-delà, les superpixels produits ont tendance à ne plus suivre les bordures des objets.
Apprentissage automatique supervisé : le séparateur à vaste marge
L'apprentissage automatique supervisé regroupe des méthodes capables d'analyser des données d'exemples (dites données d'apprentissage) et d'en déduire des règles permettant de prédire un comportement ou d'identifier la catégorie à laquelle une donnée appartient. Les séparateurs à vaste marge (SVM) font partie des méthodes les plus populaires. Initialement, ils ont été conçus pour déterminer à quelle catégorie appartient une donnée, sachant que seulement deux catégories sont possibles. La figure suivante illustre le fonctionnement d'un SVM :
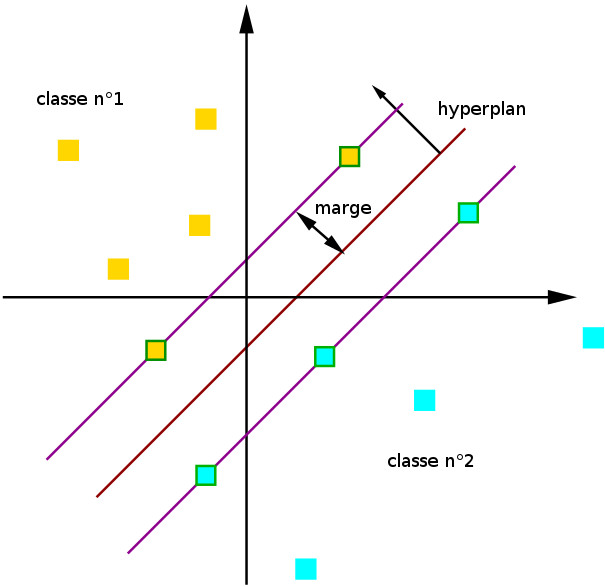
Fonctionnement d'un SVM.
Ici nos données appartiennent à deux catégories (on parle aussi de classes) : les carrés jaunes et les carrés bleus. Pour apprendre à distinguer ces deux catégories, nous fournissons au SVM une série d'exemples appartenant à chacune d'entre elles. Le SVM va chercher un hyperplan (en rouge foncé) séparant les deux classes, tout en maximisant l'écart entre l'hyperplan et les données d'exemples les plus proches de lui. Ces données sont nommées vecteurs de support. Sur notre schéma, il s'agit des rectangles bordés de vert.
Cette étape est nommée apprentissage. Une fois effectuée, de nouvelles données peuvent être classées : il suffit de regarder de quel côté de l'hyperplan elles sont positionnées.
Par la suite, de nombreuses modifications du SVM initial ont été proposées. Elles permettent notamment de gérer plus de deux classes et de calculer la probabilité d'une donnée d'appartenir à chacune des classes.
Description de chaque superpixel par un vecteur numérique
Nous allons décrire chaque superpixel par cinq valeurs numériques : trois qui correspondent à sa couleur moyenne (décrite par les quantités de rouge, de vert et de bleu) et deux qui correspondent à la position de son barycentre (dans la largeur de l'image et dans sa hauteur).
# largeur et hauteur de l'image
width = np.shape(red)[1]
height = np.shape(red)[0]
# pour calculer la position du barycentre dans la largeur de l'image
x_idx = np.repeat(range(width), height)
x_idx = np.reshape(x_idx, [width, height])
x_idx = np.transpose(x_idx)
# pour calculer la position du barycentre dans la hauteur de l'image
y_idx = np.repeat(range(height), width)
y_idx = np.reshape(y_idx, [height, width])
# extraire les caractéristiques de chaque superpixel
feature_superpixels = []
for label in range(nb_superpixels):
# pixels appartenant au superpixels
idx = superpixel_labels == label
# calcul et normalisation de la couleur moyenne
c1_mean = np.mean(red[idx]) / 255
c2_mean = np.mean(green[idx]) / 255
c3_mean = np.mean(blue[idx]) / 255
# calcul et normalisation de la position du barycentre
x_mean = np.mean(x_idx[idx]) / (width - 1)
y_mean = np.mean(y_idx[idx]) / (height - 1)
# constitution du vecteur à 5 dimension
sp = [c1_mean, c2_mean, c3_mean, x_mean, y_mean]
feature_superpixels.append(sp)
Si vous regardez attentivement le code, vous remarquerez que la couleur moyenne et la position du barycentre sont normalisées, c'est-à dire ramenées entre 0 et 1. Ce traitement est nécessaire pour que le séparateur à vaste marge puisse utiliser les valeurs numériques.
Constitution d'un ensemble de données d'apprentissage
Afin d'apprendre à identifier nos superpixels, le SVM a besoin pour chacune de nos classes de quelques superpixels lui appartenant. Nous allons fournir une autre image à notre programme. Cette image est de la même taille que l'image d'origine. Elle contient des traits de couleur :
- ceux en rouge indiquent des pixels appartenant au ciel ;
- ceux en bleu correspondent à l'arbre ;
- ceux en jaune, au sol.
En analysant cette image, nous allons pouvoir extraire pour chaque classe, quelques superpixels lui appartenant.


Indications permettant de spécifier les données d'apprentissage pour le SVM.
path_learning = 'img_learning.png'
# lire l'image indiquant quels superpixels doivent être utilisés
# pour l'apprentissage
img_learning = im.imread(path_learning)
# récupérer les canaux de couleur de l'image
red_learning = img_learning[:, :, 0]
green_learning = img_learning[:, :, 1]
blue_learning = img_learning[:, :, 2]
# récupérer la couleur associée à chaque classe
class_colors = [(red_learning[y, x], green_learning[y, x], blue_learning[y, x]) for y in range(height) \
for x in range(width)]
class_colors = set(class_colors)
class_colors.remove((0, 0, 0))
class_colors = list(class_colors)
# recupérer pour chaque classe tous les pixels qui lui sont attribués
class_pixels = []
for color in class_colors:
learning_pixels = (red_learning == color[0]) \
& (green_learning == color[1]) \
& (blue_learning == color[2])
class_pixels.append(learning_pixels)
# recupérer pour chaque classe quelques superpixels représentatifs
X = [] # caractéristiques des superpixels
Y = [] # identifiant de la classe
for label in range(nb_superpixels):
# parcour l'ensemble des pixels du
# superpixel et regarder combien
# d'entre eux sont attribués à
# chaque classe
nb_for_each_class = []
idx_sp = superpixel_labels == int(label)
for learning_pixels in class_pixels:
common_idx = np.logical_and(learning_pixels, idx_sp)
nb_for_each_class.append(np.sum(common_idx))
# tester si le superpixel contient des pixels
# appartenant à une et une seule classe
class_idx = -1
several_classes = 0
for idx in range(len(nb_for_each_class)):
if nb_for_each_class[idx] > 0:
if class_idx < 0:
# le superpixel contient
# des pixels appartenant
# à l'une des classes
class_idx = idx
else:
# le superpixel contient
# des pixels appartenant
# à plusieurs classes :
# ne pas le retenir comme
# donnée d'apprentissage
several_classes = True
# si le superpixel a été retenu comme donnée
# d'apprentissage, on stocker ses caractéristiques
# et l'identifiant de la classe
if (class_idx >= 0) and not several_classes:
Y.append(class_idx)
X.append(feature_superpixels[label])
À l'issue de cette étape nous avons donc deux tableaux :
- X, qui contient les vecteurs décrivant les superpixels utilisés lors de l'apprentissage ;
- Y, qui associe chaque superpixel à une classe.
Apprentissage
Pour créer et entraîner le SVM, nous allons utiliser la bibliothèque Scikit-image. Pour calculer la distance entre les points et l'hyperplan, plusieurs fonctions (nommées noyaux) sont disponibles. Nous allons utiliser le noyau RBF (de l'anglais Radial Basis Fonction), qui correspond à une version légèrement modifiée de la fonction exponentielle. Pour la majorité des problèmes, il donne de très bons résultats. Cette fonction RBF comprend un paramètre, dont il nous faudra spécifier la valeur. Nous aurons également à donner un paramètre gamma qui indique à quel point les données d'apprentissage sont fiables. Enfin nous précisons que le séparateur à vaste marge devra fournir les probabilités d'appartenir à chacune des classes.
# creer le séparateur à vaste marge model_svm = svm.SVC(decision_function_shape='ovo') # paramètre du SVM permettant d'influencer la proportion # de données d'apprentissage pouvant être considérées comme # erronées model_svm.C = 4. # paramètre du noyau du SVM model_svm.gamma = 4. # indiquer que les probabilités d'appartenir à chaque classe # doivent être calculées model_svm.probability = True # entraîner le SVM model_svm.fit(X, Y)
Classification
Une fois le séparateur à vaste marge entraîné, nous pouvons l'utiliser pour prédire la probabilité qu'ont les superpixels d'appartenir à chacune des classes.
# predire la probabilité de chaque superpixel # d'appartenir à chacune des classes probas = model_svm.predict_proba(feature_superpixels) # predire la classe la plus probable pour chaque superpixel classification = model_svm.predict(feature_superpixels)
Les figures suivantes correspondent aux cartes de probabilités indiquant pour chaque classe, la probabilité qu'a chaque pixel de lui appartenir. Plus le pixel apparaît en clair, plus cette probabilité est élevée. La probabilité d'un pixel d'appartenir à une classe est celle du superpixel auquel il appartient.

Probabilité d'appartenir au ciel.

Probabilité d'appartenir au sol.

Probabilité d'appartenir à l'arbre.
Ces cartes ont été générées en utilisant les bibliothèques Matplotlib et Seaborn.
# parcourir chacune des classes
for class_id in range(len(class_colors)):
pixel_probas = np.zeros([height, width])
# transférer la probabilité du superpixel
# aux pixels qui le constituent
for label in range(nb_superpixels):
idx = superpixel_labels == label
pixel_probas[idx] = probas[label, class_id]
# afficher le résultat
plt.figure(figsize=(16, 8))
sns.heatmap(pixel_probas, xticklabels=False, yticklabels=False)
plt.show()
Conclusion
Le programme que nous avons développé est relativement simple. Il illustre la puissance des bibliothèques Python pour le calcul numérique. Leur facilité d'utilisation ainsi que la profusion de méthodes disponibles permet en quelques lignes de code de réaliser des applications capables de résoudre des problèmes complexes.
Si cet exemple vous a intéressé, vous pouvez venir creuser le sujet sur l'une de nos formations en Python scientifique ou en Machine Learning !
Formations associées
Formations IA / Data Science
Formation Python scientifique
Aucune session de formation n'est prévue pour le moment.
Pour plus d'informations, n'hésitez pas à nous contacter.
Voir la Formation Python scientifiqueFormations IA / Data Science
Formation Machine Learning
Nantes - Toulouse - Paris ou distanciel A la demande
Voir la Formation Machine LearningFormations IA / Data Science
Formation Mise en place de projets Deep Learning avec Keras
Nantes - Toulouse - Paris ou distanciel A la demande
Voir la Formation Mise en place de projets Deep Learning avec KerasActualités en lien
Calculez sur GPU avec Python – Partie 3/3
Data Science
20/02/2025

Déboguer des triggers SQL en cascade – Approche Matplotlib
SQL
18/02/2025

Calculez sur GPU avec Python – Partie 2/3
Data Science
11/02/2025


